Was ist ein Venn Diagramm?
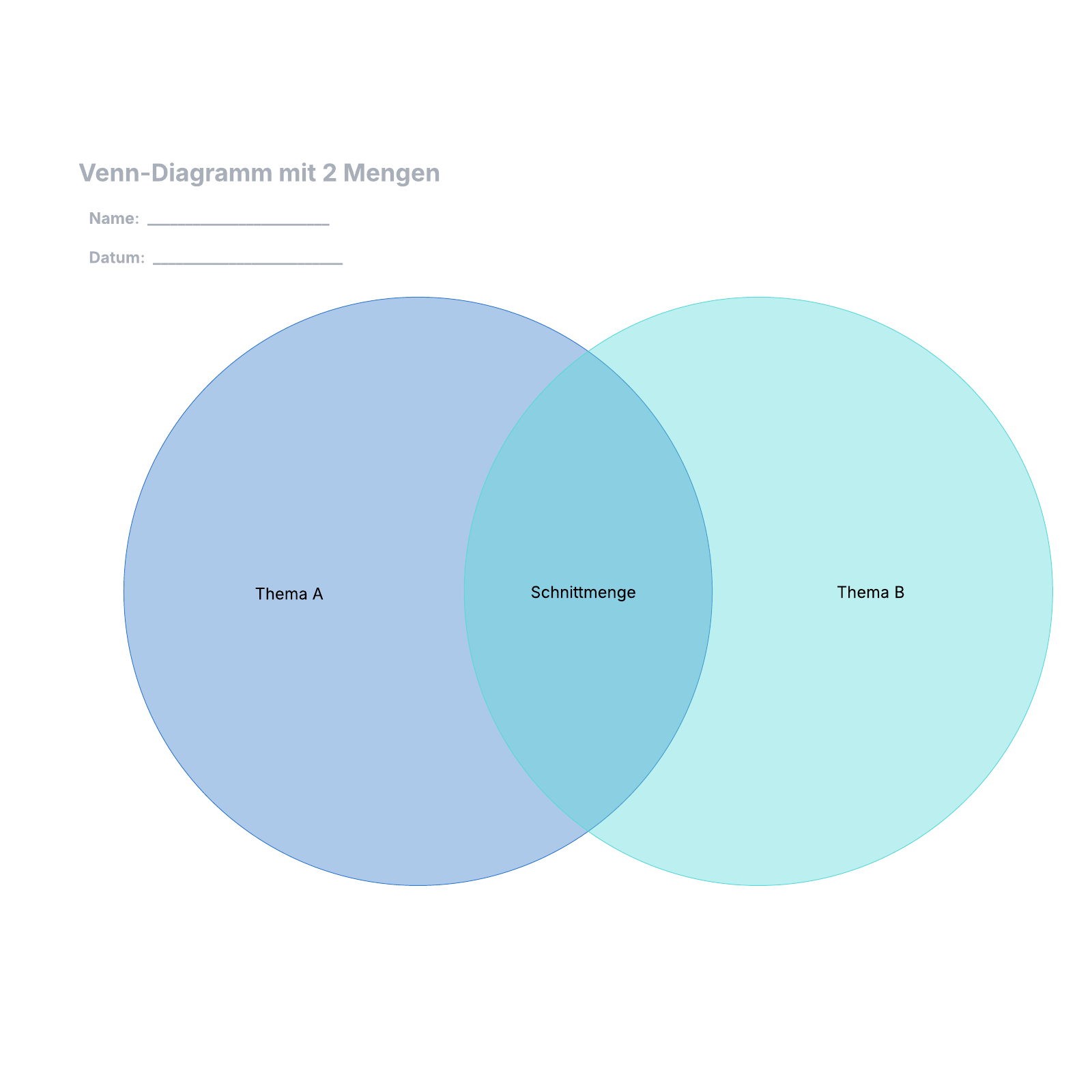
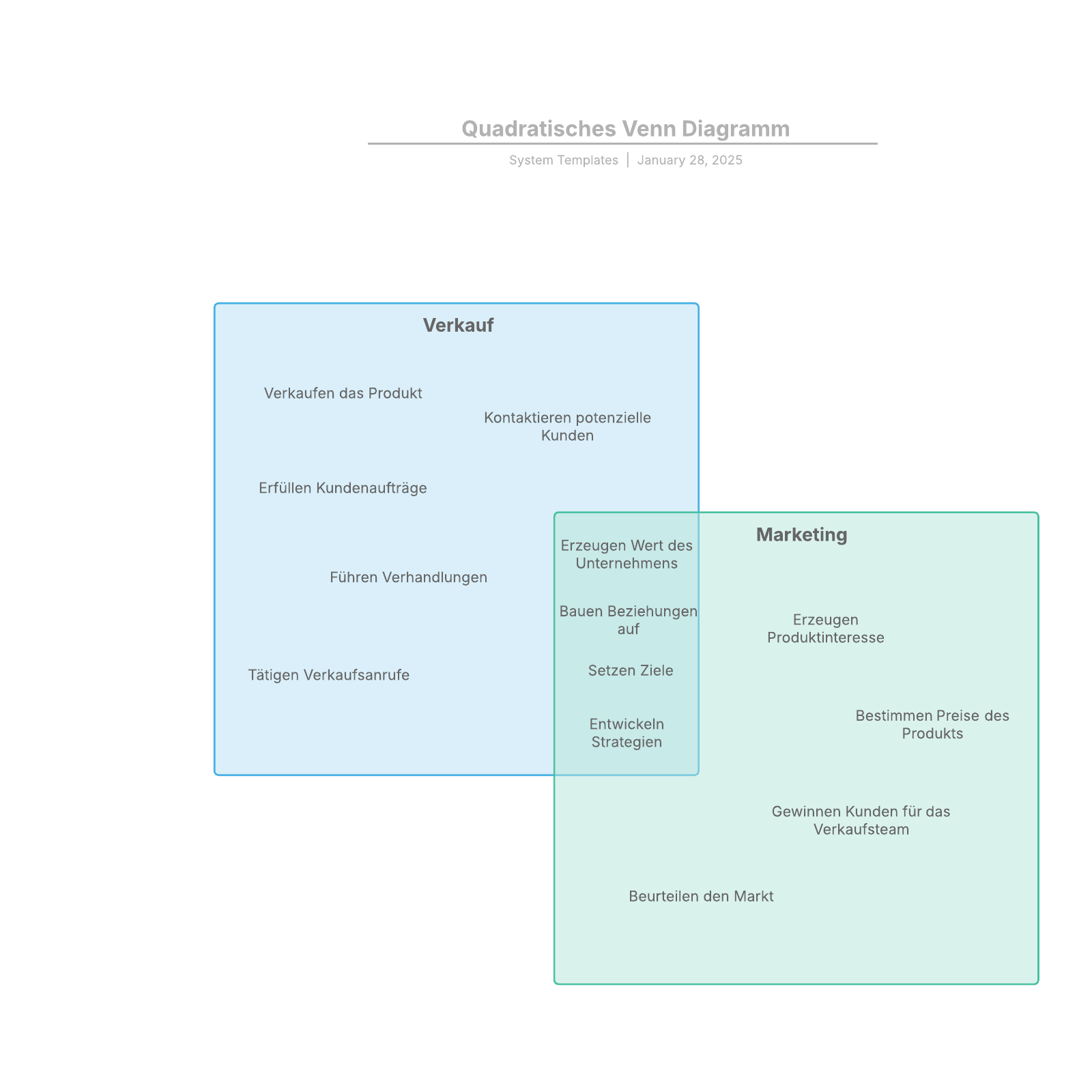
Ein Venn Diagram - auf Deutsch als Venn Diagramm bekannt - verwendet überlappende Kreise oder andere Formen, um die logische Beziehung zwischen zwei oder mehr Mengen darzustellen. Häufig dienen sie dazu, Dinge grafisch zu organisieren, indem hervorgehoben wird, worin sie sich unterscheiden und wo sie Gemeinsamkeiten besitzen.
Das Venn Diagramm in der Mengenlehre
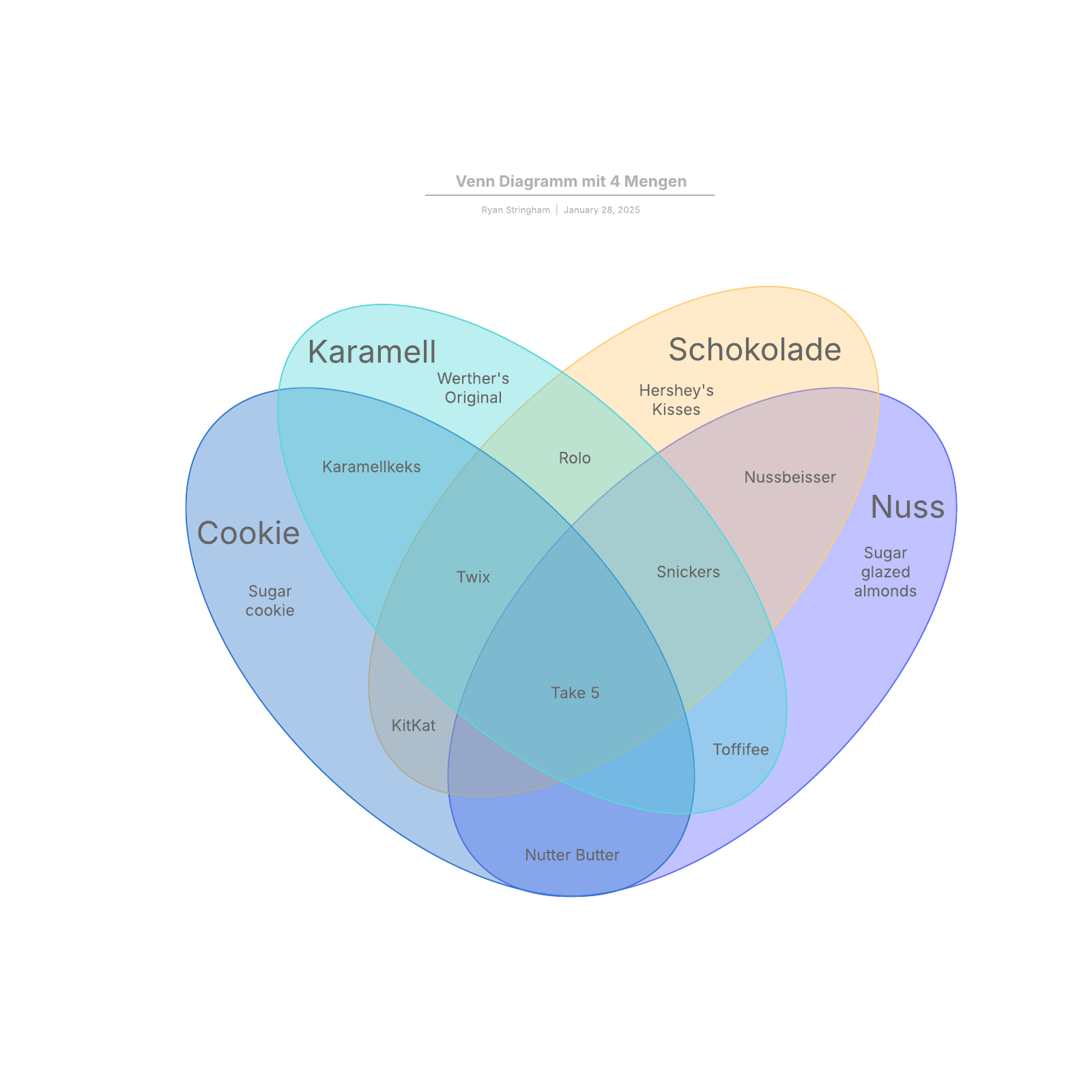
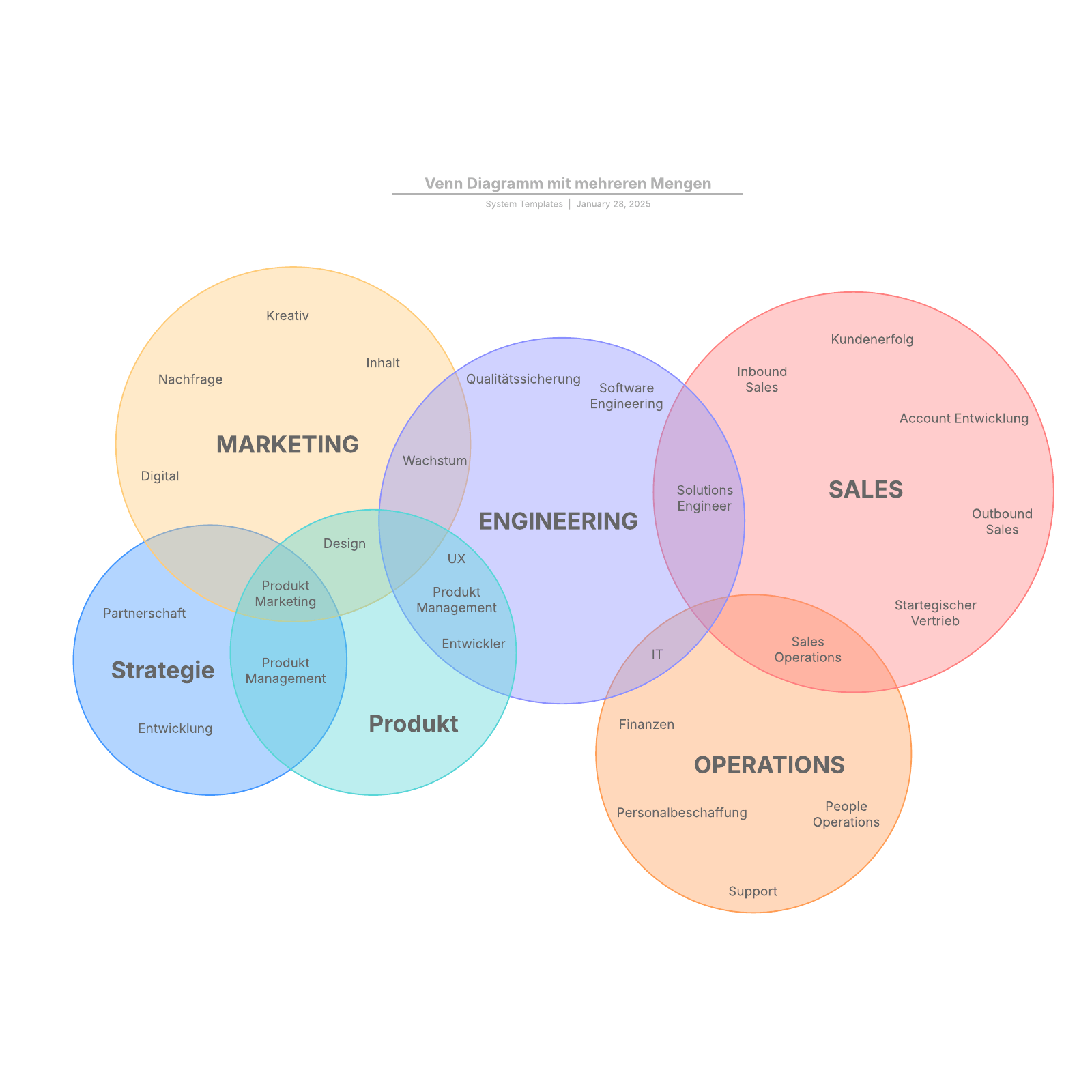
Venn Diagramm werden auch als Mengendiagramme oder logische Diagramme bezeichnet und kommen vor allem in der Mathematik, Logik, Statistik, Pädagogik, Linguistik, Informatik und im Geschäftswesen zum Einsatz. Die meisten Menschen lernen diese Diagramme bereits in der Schule im Mathematikunterricht kennen, da die Mengenlehre im Rahmen der Neuen Mathematik Einzug in Lehrpläne gehalten hat. Venn Diagramm können einfache Diagramme mit zwei oder drei Mengenelementen sein. Oder es handelt sich dabei um anspruchsvolle Diagramme, unter Umständen sogar mit 3D-Präsentationen, wenn sie sechs, sieben oder sogar mehr Mengen umfassen. Mithilfe dieser Diagramme soll illustriert werden, wie Elemente in einem bestimmten „Universum“ oder „Segment“ zueinander in Beziehung stehen. Für Benutzer sind Venn Diagramm eine hervorragende Möglichkeit, um Daten klar und effektiv zu visualisieren. Aus diesem Grund werden diese Diagramme häufig in Präsentationen und Berichten verwendet. Venn Diagramm sind eng mit dem Eulerdiagramm verwandt. In Eulerdiagrammen werden allerdings nur die tatsächlichen Überschneidungen dargestellt. In Venn Diagramm hingegen werden mögliche Überlappungen illustriert, auch wenn eine Menge leer ist.



Lernen Sie Lucidchart in weniger als 5 Minuten zu verwenden
- Zeichnen Sie Ihr erstes Venn Diagramm, oder anderes grafisches Mengendiagramm, basierend auf einer unserer fertigen Vorlagen, erstellen Sie es von Grund auf neu, oder nutzen Sie die Dokumentimportfunktion.
- Fügen Sie Formen, Verbindungslinien und Text hinzu um Ihre Diagramme robuster zu machen.
- Passen Sie Farben und Format Ihrer Mengendiagramme nach Ihren Bedürfnissen an, um diese noch lesbarer und visuell ansprechender zu gestalten.
- Lokalisieren Sie benötigte Elemente mit der Suchfunktion.
- Teilen Sie Diagramme mit Ihrem Team und beginnen Sie sofort mit der Zusammenarbeit.
Entstehungsgeschichte
Venn Diagramme sind nach dem britischen Logiker John Venn benannt. Er erwähnte diese Diagramme in einem Schriftstück mit dem Titel „On the Diagrammatic and Mechanical Representation of Propositions and Reasonings” (Über die schematische und mechanische Darstellung von Behauptungen und Schlussfolgerungen), das 1880 im Philosophical Magazine and Journal of Science erschien.

Die Ursprünge dieser Art von Diagramm reichen jedoch sehr viel weiter zurück, und zwar mindestens 600 Jahre. Im 13. Jahrhundert verwendete der Philosoph und Logiker Ramon Llull (gelegentlich auch „Lull“ geschrieben) von Mallorca eine ähnliche Art Diagramm, wie die Autorin M. E. Baron in einem 1969 erschienenen Artikel schrieb, in dem sie die Geschichte des Diagramms zurückverfolgte. Sie erwähnte außerdem den deutschen Mathematiker und Philosophen Gottfried Wilhelm von Leibnitz, da dieser im späten 17. Jahrhundert ähnliche Diagramme gezeichnet hatte.


Im 18. Jahrhundert erfand der Schweizer Mathematiker Leonard Euler das, was später als Euler-Diagramm bekannt wurde und den direkten Vorläufer des Venn Diagramms darstellt. Genauer gesagt bezeichnete John Venn seine eigenen Diagramme als Eulersche Kreise, nicht als Venn Diagramme. Der Begriff Venn Diagramme wurde erstmals vom amerikanischen Philosophen Clarence Irving (C. I.) Lewis in seinem 1918 veröffentlichten Buch „A Survey of Symbolic Logic“ (Ein Überblick über die symbolische Logik) publiziert.
Venn Diagramme haben sich im Laufe der letzten 60 Jahre kontinuierlich weiterentwickelt, wozu Experten wie David W. Henderson, Peter Hamburger, Jerrold Griggs, Charles E. „Chip“ Killian und Carla D. Savage beigetragen haben. Ihre Arbeit beschäftigte sich mit symmetrischen Venn Diagrammen und deren Beziehung zu Primzahlen, also Zahlen, die nicht durch andere Zahlen, ausgenommen 1, und sich selbst teilbar sind. Eines dieser symmetrischen Diagramme, basierend auf der Primzahl 7, ist unter Mathematikern weithin als „Victoria“ bekannt.
Weitere bedeutende Namen in der Entwicklung des Venn Diagramms sind A. W. F. Edwards, Branko Grunbaum und Henry John Stephen Smith. Sie veränderten u. a. die Formen in den Diagrammen, um eine einfachere Darstellung von Venn Diagrammen bei steigender Anzahl von Mengen zu ermöglichen.
Anwendungsbereiche
- Mathematik: Venn Diagramme werden häufig in der Schule eingesetzt, um grundlegende mathematische Konzepte wie Mengen, Vereinigungsmengen und Schnittmengen zu vermitteln. Sie werden außerdem in der höheren Mathematik verwendet, um komplexe Probleme zu lösen, und wurden in wissenschaftlichen Fachzeitschriften bereits ausführlich behandelt. Die Mengenlehre stellt einen ganzen Zweig der Mathematik dar.
- Statistik und Wahrscheinlichkeit: In der Lehre der Statistik und Wahrscheinlichkeitsrechnung verwenden Venn Diagramme verwendet, um die Wahrscheinlichkeit bestimmter Ereignisse vorherzusagen. Dies hängt mit dem Feld der prädiktiven Analytik zusammen. Verschiedene Datensätze können verglichen werden, um das jeweilige Maß an Übereinstimmungen und Unterschieden zu ermitteln.
- Logik: Venn Diagramme werden benutzt, um die Gültigkeit bestimmter Argumente und Schlussfolgerungen zu ermitteln. Wenn bei einer deduktiven (schlussfolgernden) Argumentation die Voraussetzungen wahr sind und die Form des Arguments richtig ist, dann muss auch die Schlussfolgerung wahr sein. Wenn z. B. alle Hunde Tiere sind und unser Haustier Mojo ein Hund ist, dann muss Mojo ein Tier sein. Wenn wir Variablen zuweisen, dann sagen wir, dass Hunde C sind, Tiere A sind und Mojo B ist. In Form eines Arguments würden wir sagen: Alle C sind A. B ist C. B ist daher A. Ein zugehöriges Diagramm in der Logik wird als „Wahrheitstabelle“ bezeichnet, in der die Variablen in Spalten aufgeteilt werden, um zu ermitteln, was logisch gültig ist. Ein weiteres damit zusammenhängendes Diagramm bezeichnet man als „Randolph-Diagramm“ oder R-Diagramm, nach dem Mathematiker John F. Randolph. Bei diesem werden Linien verwendet, um Mengen zu definieren.
- Linguistik: Mengendiagramme werden verwendet, um die Gemeinsamkeiten und Unterschiede zwischen Sprachen zu studieren.
- Unterrichten von Leseverständnis: Lehrer können Venn Diagramme einsetzen, um das Leseverständnis ihrer Schüler zu verbessern. Schüler können Diagramme zeichnen, um Ideen, über die sie lesen, zu vergleichen und zu kontrastieren.
- Informatik: Programmierer können Venn Diagramme nutzen, um Programmiersprachen und Hierarchien zu visualisieren.
- Wirtschaft: Venn Diagramme können verwendet werden, um Produkte, Dienstleistungen, Prozesse und mehr oder weniger alles zu vergleichen und kontrastieren, was sich als Menge darstellen lässt. Darüber hinaus sind sie ein effektives Kommunikationsmittel, um diesen Vergleich zu illustrieren.
Nicht viele Diagramme haben ihren Weg in die Popkultur gefunden – bis auf das geschätzte Venn Diagramm.
- Drama: In der CBS-Fernsehserie NUMB3RS, die von 2005 bis 2010 ausgestrahlt wurde, benutzt das Mathegenie Charles Eppes ein Venn Diagramm, um zu ermitteln, welche Verdächtigen mit einer Beschreibung übereinstimmen und für Gewaltverbrechen vorbestraft sind.
- Comedy: In der NBC-Show „Late Night with Seth Meyers“ hat der Comedian eine wiederkehrende Nummer mit dem Titel „Venn Diagramme“, in der er zwei scheinbar unverwandte Dinge vergleicht, um deren witzige Gemeinsamkeiten zu finden (so hofft er zumindest).
Venn Diagramm Bestandteile erklärt
| Menge | Eine Ansammlung von Dingen. In Anbetracht der Vielseitigkeit von Venn Diagrammen kann es sich bei diesen Dingen um praktisch alles handeln. Die Dinge können als „Elemente“, „Objekte“, „Mitglieder“ oder Ähnliches bezeichnet werden. |  |
| Vereinigung | Alle Elemente in den Mengen. |  |
| Schnittpunkt | Die Elemente in den Mengen, die sich überschneiden. Gelegentlich auch als Teilmenge bezeichnet. |  |
| Symmetrische Differenz von zwei Mengen | Alles außer der Schnittmenge. |  |
| Absolutes Komplement | Alles, das sich nicht in der Menge befindet. |  |
| Relatives Komplement | In einer Menge, aber nicht in der anderen. |  |
| Skaliertes Venn Diagramm | Auch als „flächenproportional“ bezeichnet. Die Größe der Kreise (oder anderen Formen) richtet sich nach ihrem proportionalen Anteil am Ganzen. |  |
| Reuleaux-Dreieck | Form, die durch die Schnittmenge von drei Kreisen oder Formen gebildet wird, z. B. in einem Venn Diagramm. |  |
| Mengenbezeichnungen |
Die in Venn Diagrammen abgebildeten Konzepte werden in mathematischer Notation ausgedrückt, z. B. die Bezeichnungen für Mengen und Teilmengen (in Klammern), Vereinigungsmengen (mit einem U-artigen Symbol) und Schnittmengen (mit einem umgedrehten U-Symbol). | |
| Mengenlehre | Der altehrwürdige Zweig der Mathematik, der sich mit Mengen beschäftigt. |
Verwendungszwecke und Vorteile
- Um Informationen visuell zu organisieren und so die Beziehungen zwischen Mengen bestimmter Gruppen sichtbar zu machen, wie z. B. Gemeinsamkeiten und Unterschiede. Studierende und Fachexperten können von ihnen Gebrauch machen, um die Logik hinter einem Konzept zu durchdenken und die Beziehungen im Rahmen visueller Kommunikation abzubilden. Dieser Zweck kann diverse Anwendungsbereiche umfassen – von grundlegend bis hochkomplex.
- Um zwei oder mehr Optionen zu vergleichen und deutlich sichtbar zu machen, was diese gemeinsam haben und worin sie sich unterscheiden. Dies kann beispielsweise im Rahmen der Kaufentscheidung für ein wichtiges Produkt oder eine Dienstleistung erfolgen.
- Um komplexe mathematische Aufgaben zu lösen. Vorausgesetzt natürlich, dass Sie Mathematiker sind.
- Um Datensätze zu vergleichen, Zusammenhänge zu finden und bestimmte Eintrittswahrscheinlichkeiten vorauszusagen.
- Um die Logik hinter Aussagen oder Gleichungen zu begründen, z. B. die Boolesche Logik hinter einer Wortsuche, die „oder“ und „und“-Aussagen beinhaltet, und wie diese gruppiert sind.
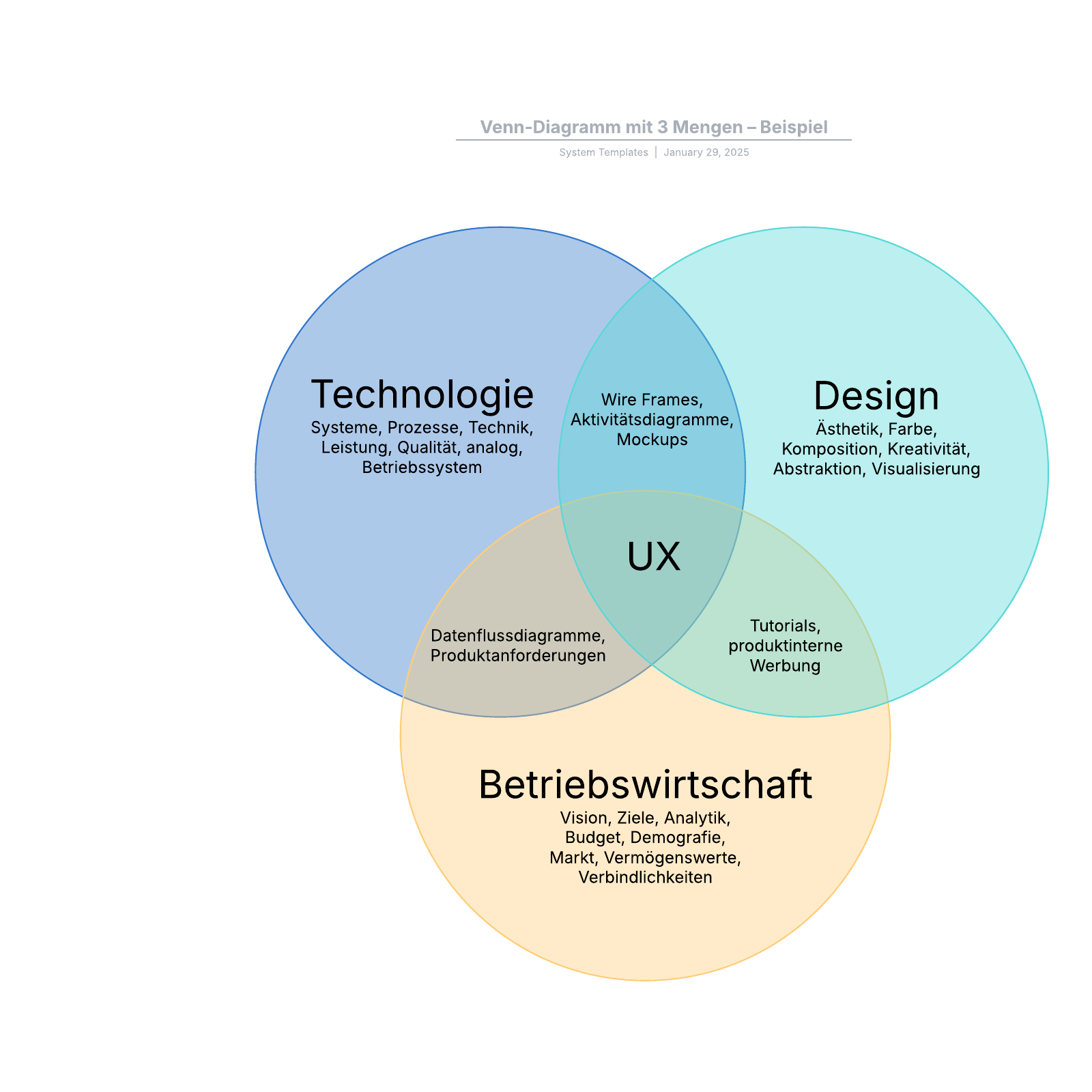
Drei Mengen Venn Diagramm Beispiel mit Erklärung
Nehmen wir an, unser Universum ist „Haustiere“, und wir möchten ermitteln, auf welche Art von Haustier unsere Familie sich einigen könnte.
Die Menge „A“ enthält meine Präferenzen: Hund, Vogel, Hamster.
Die Menge „B“ enthält die Präferenzen von Familienmitglied B: Hund, Katze, Fisch.
Die Menge „C“ enthält die Präferenzen von Familienmitglied C: Hund, Katze, Schildkröte, Schlange.
Im Überlappungsbereich, oder der Schnittmenge, der drei Mengen befindet sich nur „Hund“. Sieht so aus, als ob wir uns einen Hund anschaffen.
Natürlich kann die Komplexität von Venn Diagrammen weit über dieses Beispiel hinausgehen, da sie in diversen Fachgebieten häufig verwendet werden.
Schritte zum Zeichnen und Verwenden eines einfachen Venn Diagramms
- Bestimmen Sie Ihr Ziel. Was vergleichen Sie, und warum? Das wird Ihnen helfen, Ihre Mengen zu definieren.
- Machen Sie ein Brainstorming und listen Sie die Elemente in Ihren Mengen auf, entweder auf Papier oder mithilfe einer Plattform spezialisiert auf das Erstellen von Venn Diagrammen wie Lucidchart.
- Verwenden Sie nun Ihr Diagramm, um die Mengen zu vergleichen und zu kontrastieren. So können Sie die Dinge womöglich aus einer neuen Perspektive betrachten und neue Aspekte entdecken, Entscheidungen treffen oder Argumente finden.
So erstellen Sie ein Venn Diagramm in PowerPoint
1. Öffnen Sie eine neue Präsentation in PowerPoint.
2. Ändern Sie das Layout, um eine leere Arbeitsfläche zu schaffen. Gehen Sie unter Start zu Layout und wählen Sie die Option Leere Präsentation.
3. Klicken Sie auf den Tab Einfügen und wählen Sie SmartArt.
Venn Diagramm in PowerPoint formatieren
TEXT HINZUFÜGEN
Sobald Sie die gewünschte Grafik in SmartArt ausgewählt haben, wird ein Dialogfenster angezeigt, mit dem Sie Ihrem Venn Diagramm Text hinzufügen können. Anhand der Liste mit den Stichpunkten können Sie die Textfelder für jeden Kreis ausfüllen.

Den Stil Ihres Venn Diagramms anpassen
Klicken Sie mit der rechten Maustaste auf einen der Kreise in Ihrem Venn Diagramm. Wählen Sie die Option Form formatieren. Daraufhin öffnet sich auf der rechten Seite ein Menü mit Formatierungsoptionen für Text und Form. Versuchen Sie, die Farbe zu ändern – wir haben den obersten Kreis rot gefärbt.

Design anpassen
Das Standardlayout lässt sich ganz leicht aufpeppen: Klicken Sie dafür einfach auf den Tab Entwurf. In diesem Beispiel haben wir das erste Design beibehalten, aber als Hintergrundformat haben wir die dritte Variante gewählt: schwarzer Hintergrund, weißer Text und weiße Kreisumrisse sowie verschiedene Farbtöne für die Kreise.
So sieht das Venn Diagramm letztendlich in PowerPoint aus:

Nehmen wir einmal an, dass wir unser Venn Diagramm nicht als PPT Datei, sondern als PNG Bild speichern möchten. Gehen Sie dazu auf Datei > Exportieren > Dateityp ändern.
Venn Diagramme in Lucidchart erstellen
Lucidchart verfügt über mehrere nützliche Funktionen, die in PowerPoint nicht verfügbar sind und die Ihnen wesentlich mehr Flexibilität bei der Erstellung eines ansprechenden Venn Diagramms bieten. So können Sie Ihr Venn Diagramm nach Herzenslust anpassen und sind auf dem besten Wege, beeindruckende, professionell aussehende Venn Diagramme zu erstellen.
Befolgen Sie diese einfachen Schritte, um eindrucksvolle Diagramme zu erstellen:
1. Richten Sie ein kostenloses Lucidchart Konto ein
Ein Klick sowie die Angabe einer E-Mail-Adresse genügen, um ein neues Konto bei Lucidchart einzurichten. Klicken Sie dazu einfach hier – der Vorgang dauert in der Regel weniger als eine Minute.
2. Hinzufügen von Formen oder Verwendung einer Vorlage
In Lucidchart gibt es mehrere Möglichkeiten zur Erstellung eines Venn Diagramms. Für eine manuelle Erstellung können Sie per Drag-and-drop Kreise einfügen. Alternativ dazu können Sie eine unserer großartigen Vorlagen verwenden, um sofort loszulegen.
Hinzufügen von Formen
-
Stellen Sie sicher, dass Sie die richtigen Formenbibliotheken geöffnet haben, indem Sie auf die Schaltfläche „+ Formen“ klicken und die Bibliotheken für Venn Diagramme auswählen.
-
Ziehen Sie einfach eine Form aus der Toolbox auf der linken Seite auf Ihre Arbeitsfläche.
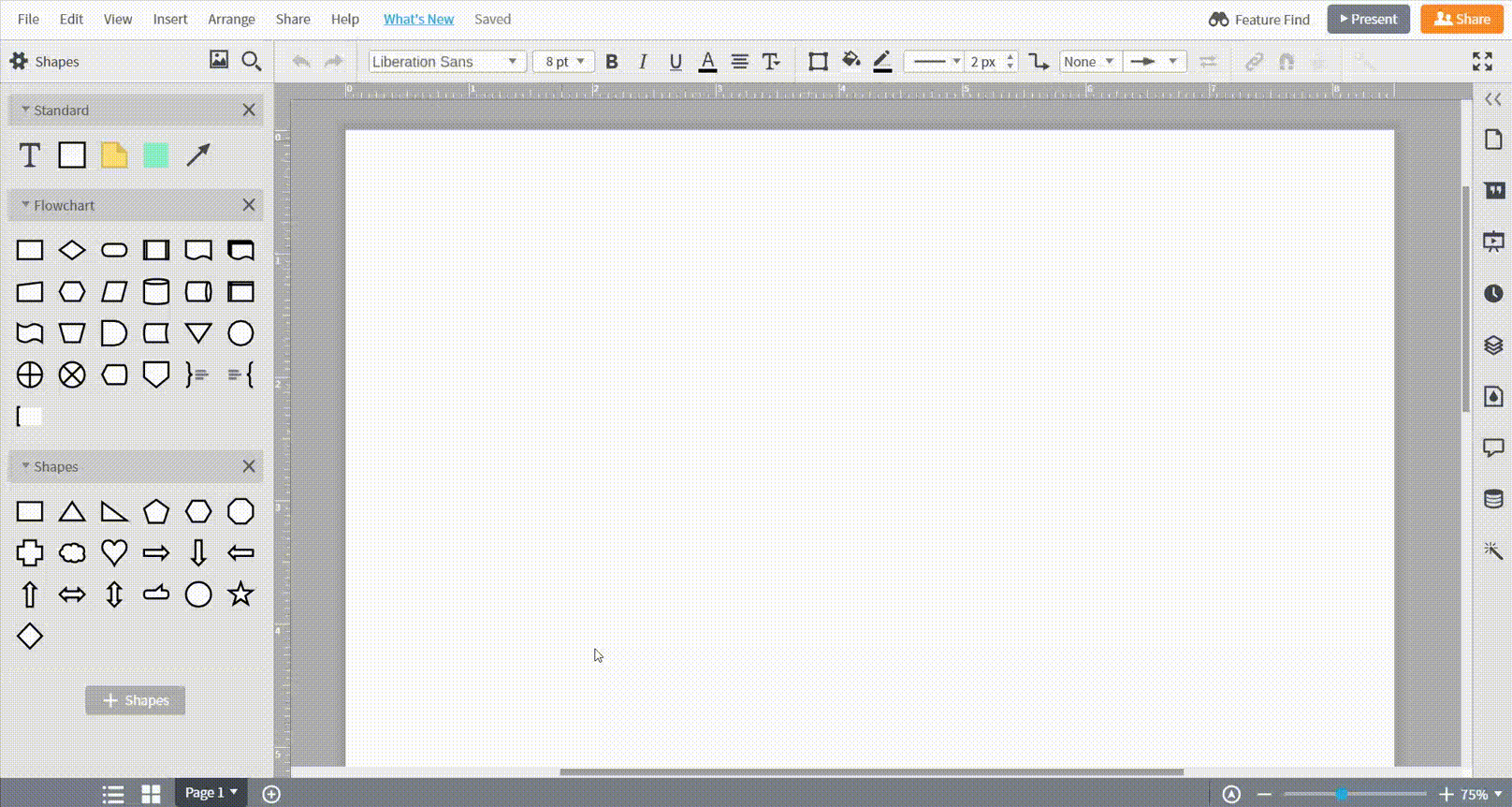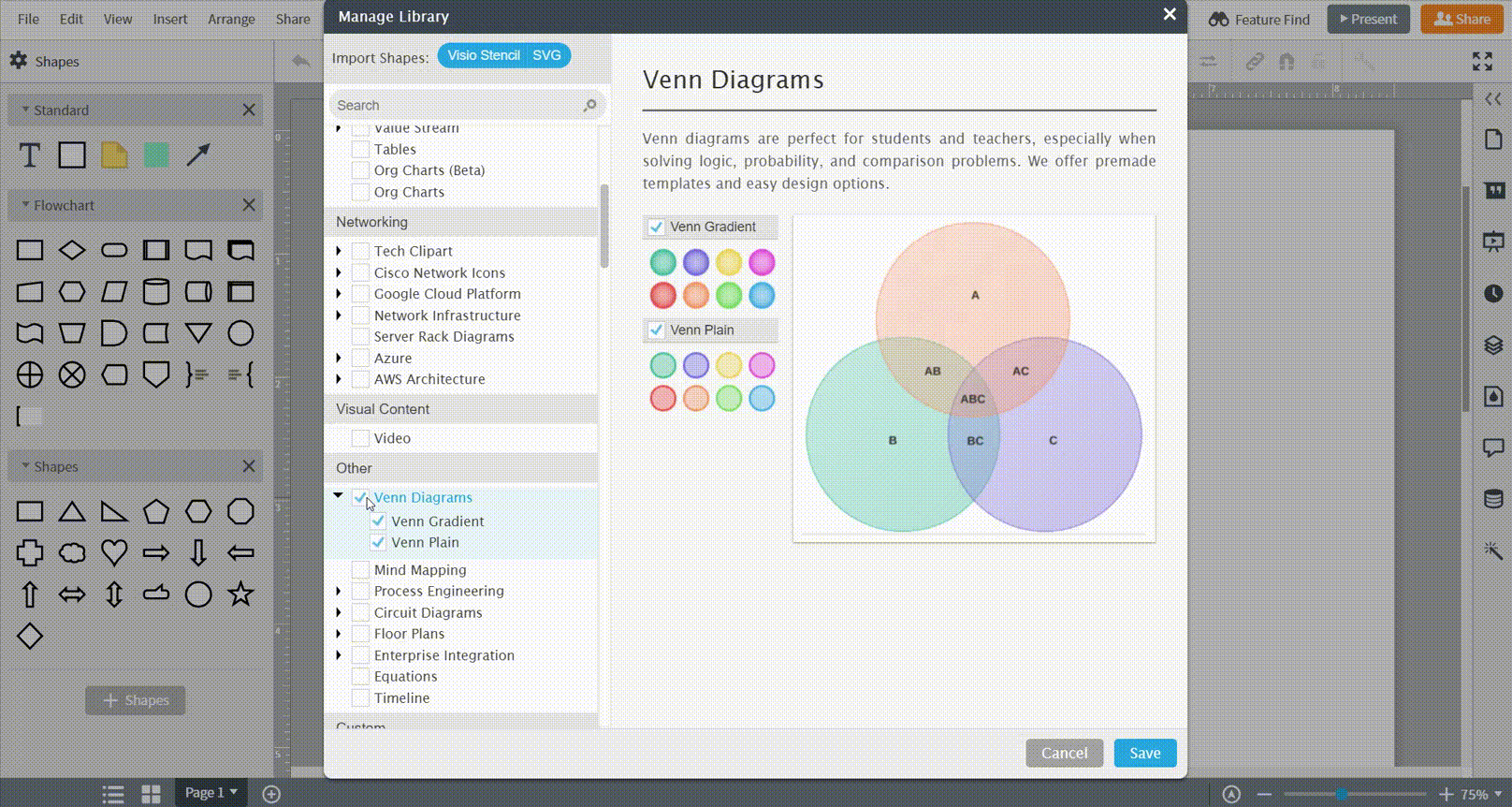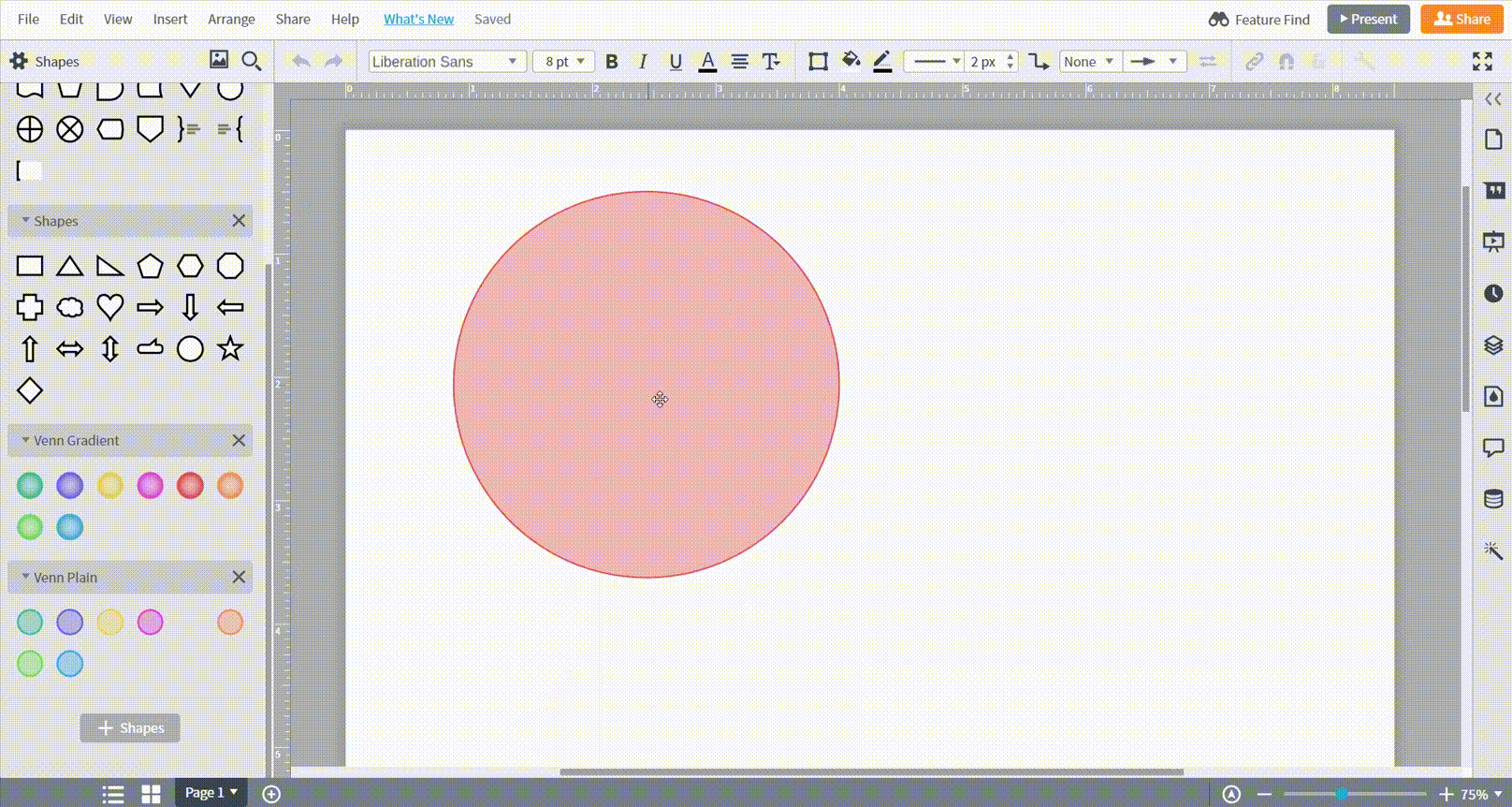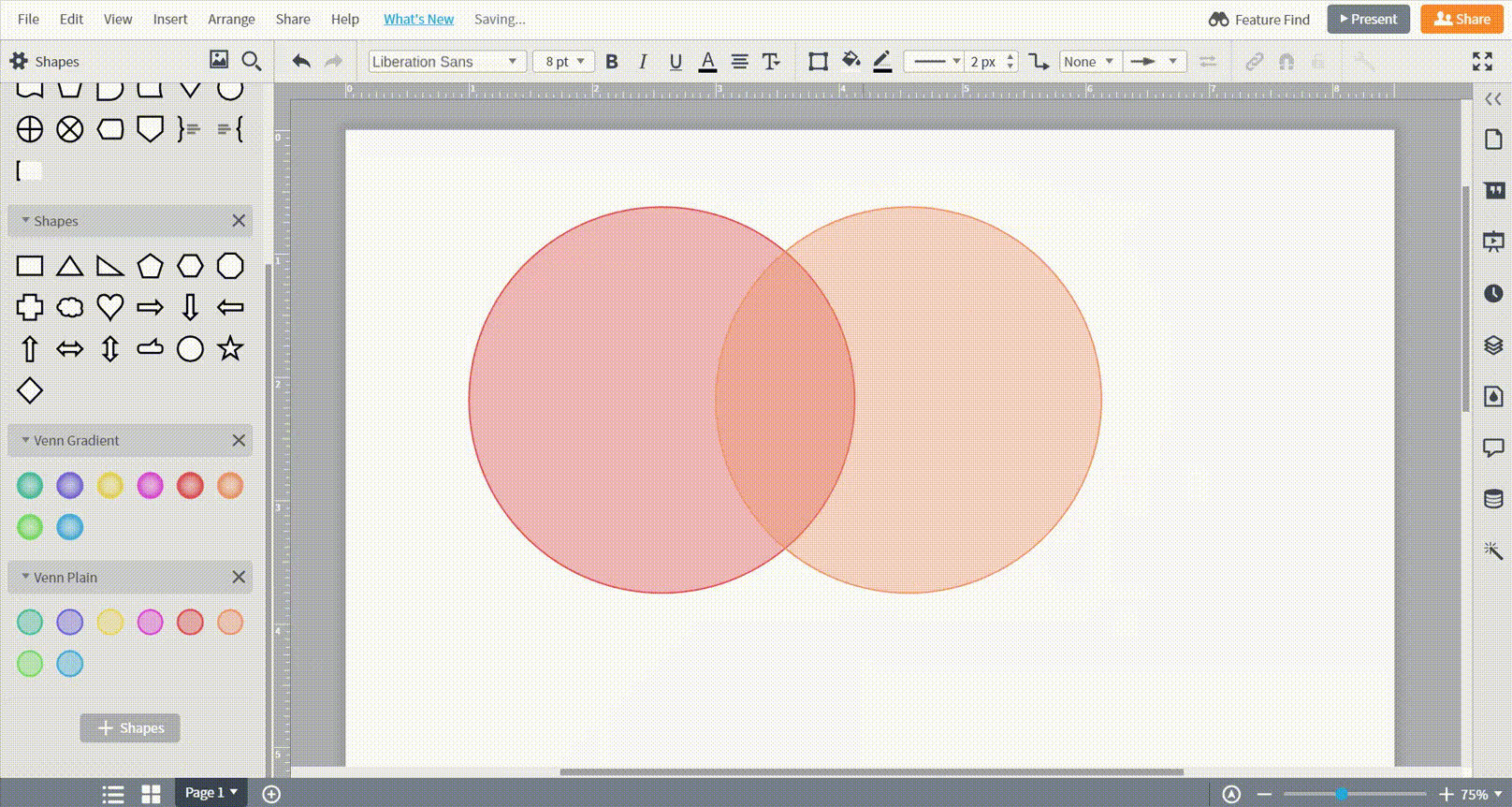
Verwendung einer Vorlage
-
Klicken Sie in der Dokumentenwarteschlange von Lucidchart auf den nach unten zeigenden Pfeil neben der orangefarbenen Schaltfläche „+ Dokument“.
-
Klicken Sie auf die Vorlagenbibliothek „Venn Diagramm“ auf der rechten Seite des Bildschirms und wählen Sie die gewünschte Vorlage aus!
3. Den Stil Ihres Venn Diagramms anpassen
Verleihen Sie Ihrem Venn Diagramm eine persönliche Note, indem Sie eigene Farben und Stile hinzufügen. Die Elemente des Venn Diagramms können genau wie andere Formen bearbeitet werden. Sie können die Farben, den Umrandungsstil, die Dicke der Umrandung und vieles mehr ändern.
-
Für eine schnelle Bearbeitung klicken Sie mit der rechten Maustaste auf eine Form. Daraufhin öffnet sich ein Menü mit beliebten Bearbeitungsoptionen, wie das Vor- oder Zurückstellen eines Objekts, das Zeichnen einer Linie oder das Wechseln der Form.
-
Um eine Form zu verschieben, klicken Sie darauf und ziehen Sie sie an die gewünschte Position. Zum Skalieren ziehen Sie an einer Kante oder Ecke. Zum Drehen klicken Sie auf das Drehsymbol und ziehen es in die gewünschte Richtung.
-
Wenn Sie mehrere Formen gemeinsam verschieben möchten, wählen Sie sie aus, indem Sie die Umschalttaste gedrückt halten, jedes Objekt anklicken und sie dann zusammen an die gewünschte Stelle ziehen.
-
Um Text zu verändern, einschließlich Ausrichtung und Schriftgröße, markieren Sie den Text und wählen Sie anschließend die gewünschten Optionen aus der Eigenschaftenleiste oben auf der Seite aus.
-
Wenn Sie Grafikeigenschaften wie Füllfarbe und Farbverläufe verändern möchten, markieren Sie das gewünschte Element und wählen Sie anschließend die entsprechenden Optionen aus der Eigenschaftsleiste oben auf der Seite aus.