ベン図とは?
ベン図とは、複数の集合(グループ)同士の関係を視覚的に表す図です。
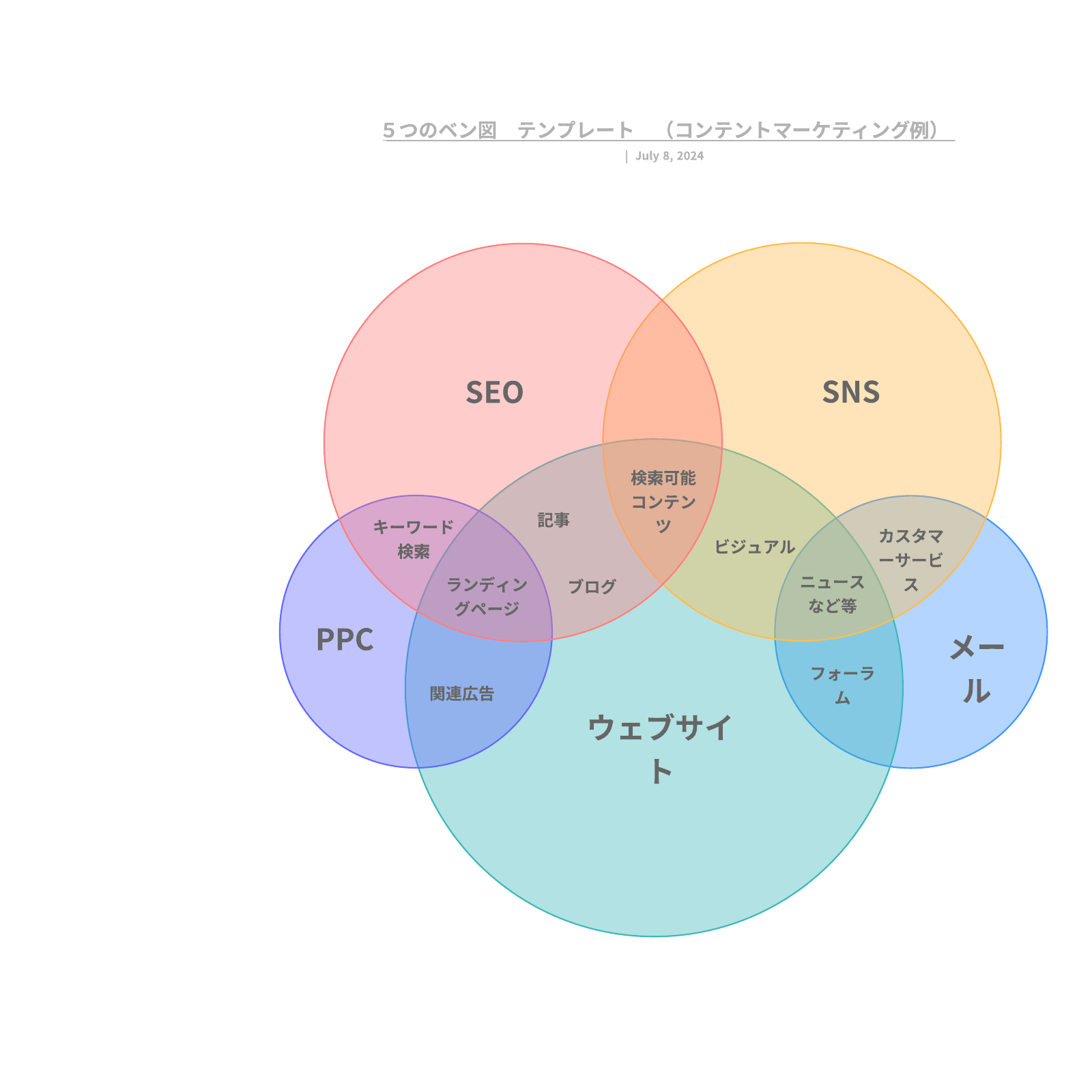
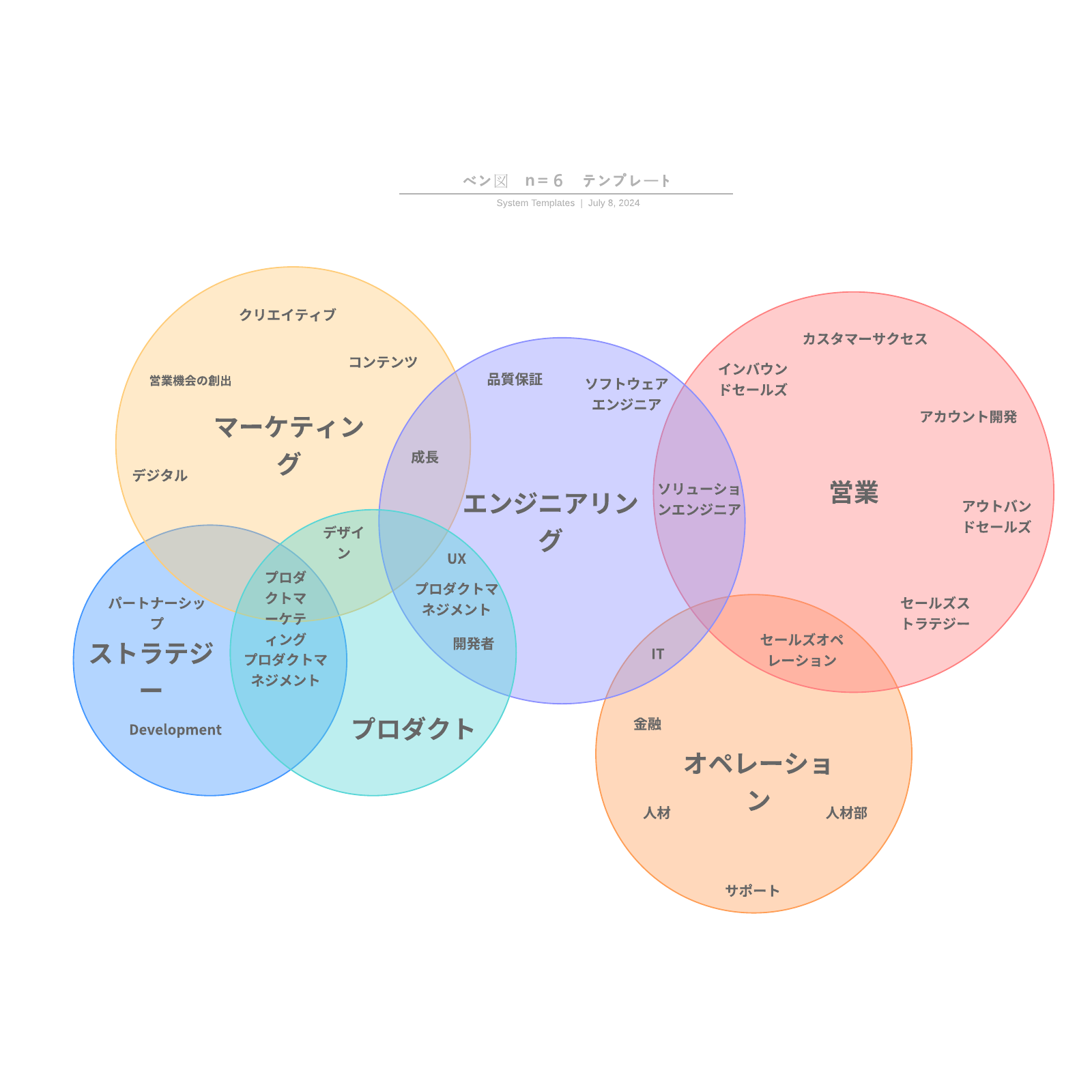
円や他の図形を使って、それぞれの集合の重なりや違いを示します。2つまたは3つの集合の関係を示す簡単なものから、6つ以上の複雑な関係を表すものまであります。項目同士がどのようにつながっているかを一目で理解できるため、プレゼンテーションやレポートなどでよく使われます。
ベン図は英語で「Venn Diagram(ベン・ダイアグラム)」と呼ばれ、日本語では「集合図」や「論理図」とも言われます。数学、統計学、論理学、教育、言語学、コンピューターサイエンス、ビジネス分野など、さまざまな分野で広く活用されています。1960年代には「新数学」のカリキュラムにも取り入れられ、多くの人が授業で目にしたことがあるでしょう。
ベン図とよく似た図に「オイラー図」がありますが、両者には違いがあります。オイラー図では、要素が存在しない部分(空集合)は省略されます。一方で、ベン図ではたとえその領域に何も含まれていなくても、すべての関係を示すために領域が残されています。
このように、ベン図は項目間の共通点や違いを整理し、視覚的にわかりやすく伝えるための有効なツールです。



ベン図のメリット
学生からビジネスパーソンまで、幅広い人たちが概念の背景にある考え方を深く理解し、その関係性をわかりやすく伝えるために活用できます。シンプルな比較から高度な分析まで、さまざまな場面で使えます。
主な活用例は以下の通りです:
-
選択肢の比較: 複数の選択肢を比較し、それぞれの共通点と相違点を明確にするために使えます。たとえば、製品やサービスを購入する際の検討に役立ちます。
-
数学の問題解決: ベン図は、特に集合や確率に関する複雑な数学の問題を整理して解くのに効果的です。数学者や学生によく利用されています。
-
データ分析: 複数のデータセットを比較し、相関関係を探ったり、ある出来事の発生確率を予測したりする際にも使われます。
-
論理的思考の補助: 「AND」や「OR」といったブール論理の理解にも役立ちます。検索や情報のグルーピング、命題や方程式の背後にある論理構造を視覚的に把握するのに便利です。
ベン図の活用場面
数学
ベン図は、集合、和集合、共通部分といった基本的な集合論の概念を教えるために、学校教育で広く活用されています。さらに、大学レベルや研究分野においても、複雑な問題の可視化や解決手段として利用さ��れ、学術論文のテーマとしても頻繁に取り上げられています。集合論自体が数学全体の基礎であり、その学習や応用においてベン図は重要な役割を果たしています。
統計・確率
統計学や確率論の分野では、ベン図を用いて異なる事象の関係性を視覚化し、特定の事象が発生する可能性を予測します。予測分析とも深く関わりがあり、複数のデータセットを比較することで、共通点と相違点の把握が可能になります。
論理学
論理学では、ベン図を使って命題の妥当性や論理的関係を視覚的に分析することができます。たとえば、「すべての犬は動物であり、モジョは犬である。したがって、モジョは動物である」という演繹的推論は、ベン図を使うことで直感的に理解できます。これを記号で表すと、「すべてのCはAである」「BはCである」「ゆえにBはAである」となります。関連する図としては、論理式の正しさを検証する「真理値表」や、集合の関係を線で表現する「ランドルフ図(R図)」などがあります。
言語学
ベン図は、複数の言語における語彙や文法構造の共通点と相違点を比較・分析するために利用されます。言語間の構造的関係を明確にするための視覚的な手段として有効です。
読解指導
読��解力の指導においても、ベン図は効果的なツールです。教師は、生徒が読書を通じて得た情報や登場人物の特徴、テーマなどを比較・対比する活動にベン図を活用し、理解を深めさせることができます。
コンピューターサイエンス
プログラミングや情報科学の分野では、異なるプログラミング言語やその機能の重複・違いを視覚化するためにベン図が使われます。階層構造やカテゴリ分けを理解する手段としても有効です。
ビジネス
ビジネスの現場では、製品、サービス、業務プロセスなどを比較・分析するための視覚的ツールとしてベン図が活用されています。複雑な関係性や差異を簡潔に伝えるためのコミュニケーション手段として、プレゼンテーションや報告資料でも重宝されています。
ベン図の書き方
1. 比較の目的を明確にする
まず、何を比較したいのかをはっきりさせましょう。対象は物事、概念、グループなど何でも構いません。
-
例:異なる製品の機能、文学作品のテーマ、動物の特徴など。
このステップでは、「どのような視点で比べるのか」「何のために比較するのか」を考えることで、後の作業で扱う“集合”を正確に定義できます。
2. 項目を洗い出す
次に、各対象に含める特徴や要素をできるだけ多くリストアップします。これは「ブレインストーミング」の段階で、制限せず自由に書き出すのがポイントです。
-
紙とペンでも、付箋でも、頭の中のメモでもOKです。
このステップでは、「どの項目がどの対象に属しているか」を後で判断しやすくするための素材を集めます。
3. 図にして可視化する
集めた項目を使って、ベン図を描いてみましょう。対象ごとに円を描き、重なりのある部分に共通項目を、円の外側には固有の項目を書きます。
-
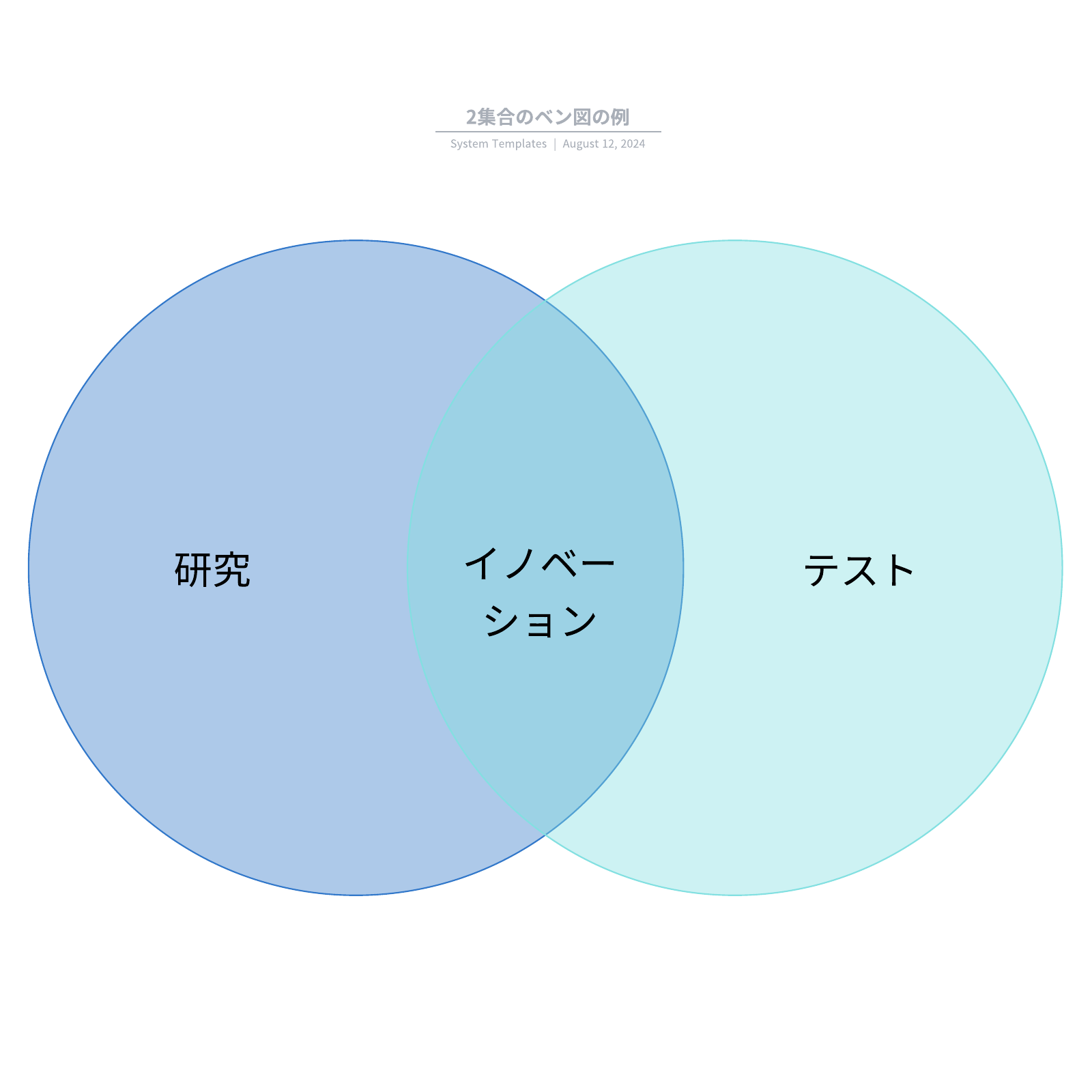
2つの円なら「共通点」と「相違点」の整理に。
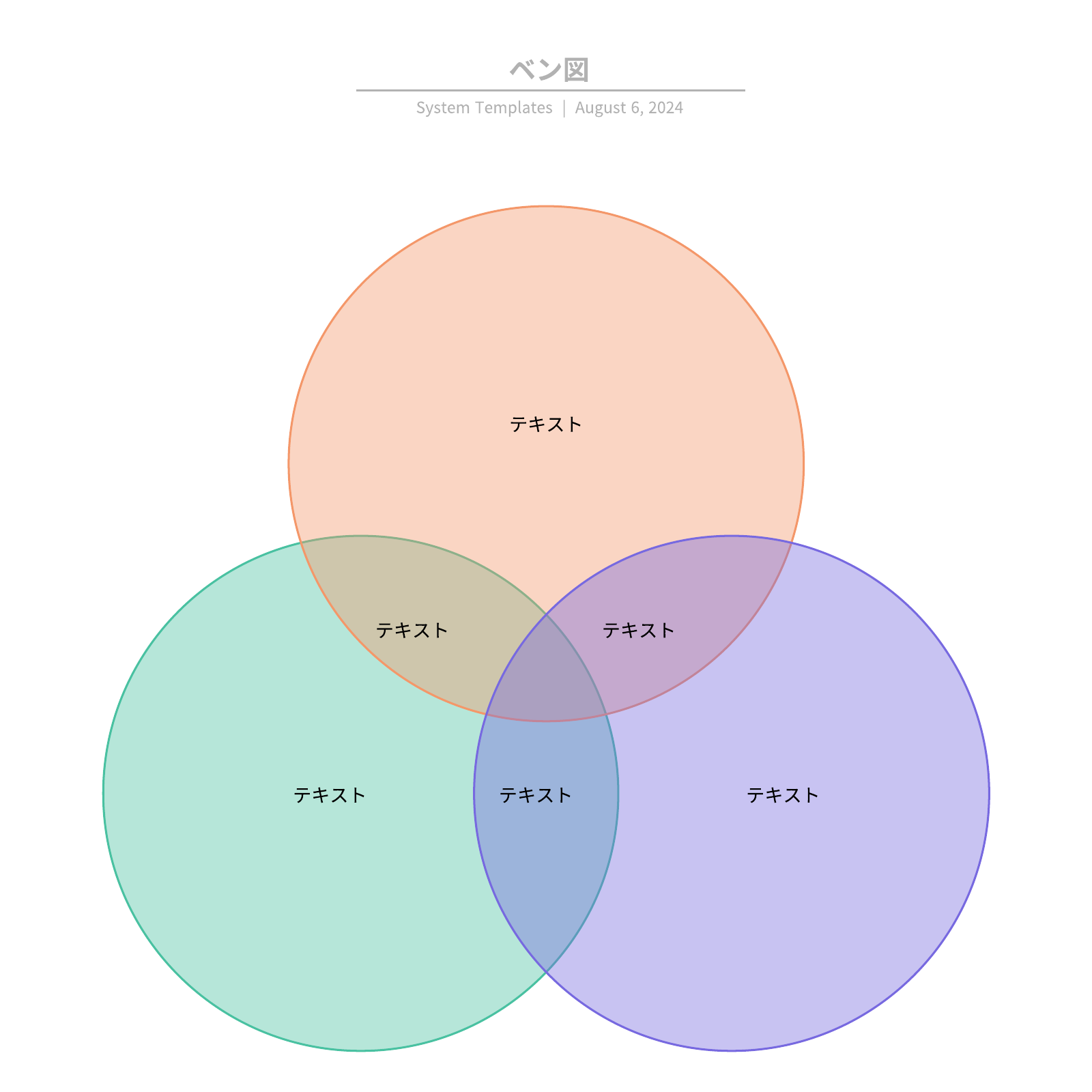
-
3つの円なら「それぞれの特徴」と「重なりのパターン」が一目で分かります。
視覚的に整理することで、次のようなことが可能になります:
-
情報の共通点や違いの発見
-
新しい視点からの観察
-
選択肢の比較と優先順位付け
-
グループでの議論や意思決定の材料として活用
この書き方は、教育、ビジネス、日常の意思決定など、さまざまな場面で活用できます。手書きでも、オンライン作図ツールでも、本質は「情報を整理して、比べて、考える」ことにあります。
ベン図の例
では、ペットを領域とし、家族が賛成してくれるようなペットを比較検討するというテーマで図を作成してみましょう。
集合 A には私の飼いたいペット、犬 (dog)、鳥 (bird)、ハムスター (hamster) が含まれます。
集合 B には家族 B の飼いたいペット、犬 (dog)、猫 (cat)、魚 (fish) が含まれます。
集合 C には家族 C の飼いたいペット、犬 (dog)、猫 (cat)、カメ (turtle)、ヘビ (snake) が含まれます。
3つの集合の重複する共通部分には、犬のみが含まれます。というわけで、おそらく犬を飼うことになるでしょう。
もちろん、これよりも大幅に複雑なベン図も多数あり、さまざまな分野で広く利用されています。
知っておきたいベン図の用語・集合記号の意味
| 集合 | 事物の集合を指します。ベン図は汎用性の高いものであり、どんな事物にでも適用することができます。この事物は、項目、オブジェクトやメンバーなどと呼ばれることもあります。 |  |
| 和集合 | 対象の集合内のすべての項目。 |  |
| 共通部分 | 対象の集合内の重複する項目。副集合と呼ばれることもあります。 |  |
| 2つの集合の対称差 | 共通部分を除くすべて。 |  |
| 絶対補集合 | 集合に含まれないすべて。 |  |
| 相対補集合 | 1つの集合に含まれ、他の集合に含まれないもの。 |  |
| 拡大型ベン図 | 面積比例とも呼ばれます。円 (またはその他の図形) のサイズが全体比で決まります。 |  |
| ルーローの三角形 | ベン図で見られるように、3つの円や図形の交点に形成される図形。 |  |
| 集合の表記 |
ベン図で表される概念は、集合や副集合 (カッコ表記)、和集合 (U 記号) や共通部分 (U を逆にした記号) などの数学的記法で表記されます。 | |
| 集合論 | 集合を取り扱う数学の一分野で、長い歴史をもちます。 |
ベン図の歴史と名前の由来
ベン図は、英国の論理学者ジョン・ベンにちなんで命名されました。同氏は、フィロソフィカル・マガジン・アンド・ジャーナル・オブ・サイエンスで発表された1880年の論文「On the Diagrammatic and Mechanical Representation of Propositions and Reasonings (定理及び推論の図式的及び機械的表現について)」でベン図について記しています。

しかし、こうした図の起源はさらに古く、少なくともこの600年前にはすでに存在したものとされています。1200年代には、哲学者で、論理学者でもあったマヨルカ島のラモン・リュイが同様の図を使用していたと、ベン図の起源をたどる1969年の論文で M・E・バロンが記しています。また、ドイツ人の数学者で、哲学者でもあったゴットフリート・ヴィルヘルム・フォン・ライプニッツが1600年代後半に類似の図を作成していたことについても触れています。.


1700年代には、スイス人の数学者レオンハルト・オイラーにより、ベン図の前身とされるオイラー図が発明されました。実際に、ジョン・ベンは、自らの図をベン図ではなくオイラー円と呼んでいます。ベン図という用語が最初に文献に現れたのは、米国人哲学者のクラランス・アーヴィング・ルイスによる1918年の著作「記号論理学の研究 (A Survey of Symbolic Logic)」の中のことです。
過去60年間、デイビット・W・ヘンダーソン、ピーター・ハンバーガー、ジェロルド・グリッグス、チャールズ・E・「チップ」キリアン、カーラ・D・サヴェージなどの専門家の尽力により、ベン図は進化を続けてきました。 こうした研究の中には、左右対称のベン図と素数 (1と自分自身以外に正の約数を持たない自然数) の関係に関するものが含まれます。こうした対称図で、素数である7に基づくものは、数学界で「ヴィクトリア」として広く知られています。
この他にも、A・W・F・エドワーズ、ブランコ・グレンバウムやヘンリー・ジョン・ステファン・スミスといった著名人がベン図の発展に寄与しています。その功績には、集合の数が増えてもシンプルに描画ができるよう、ベン図に使用する図形の形状を変更した点などがあります。
Lucidchart を使ってベン図(Venn Diagram)を簡単に作成
Lucidchart のアカウントをお持ちでない方には、無料で登録することをおすすめします。
ログインし、テンプレートを選択するか、文書を新規作成します。
Lucidchart のインポート機能を使い、Visio, Excel, PowerPoint などの他の作図プラットフォームから既存の図をインポートして作成途中の文書を共同編集したり、作業を続行することも可能です。
エクセルでのベン図の書き方
-
新しい エクセルブックを開きます。
-
シートの列に図に含めたいカテゴリーのリストを入力します。
-
[挿入] タブから [SmartArt] をクリックして SmartArt でベン図の作成を始めます。SmartArt グラフィックメニューが開きます。
-
[集合関係] メニューで使用したいベン図テンプレートを選択します。
エクセルでのベン図のスタイル設定方法:
- タイトルの追加
タイトルを追加するには、ベン図テンプレートの選択後に表示されるメニューにテキストを入力します。入力後、フォント、サイズや色など、通常のテキストと同様にタイトルを書式設定することができます。
- ベン図への円の追加
比較する変数を増やしたい場合には、図に円を追加するのが便利です。以下の手段で簡単に追加することができます。
-
-
図をクリックします。
-
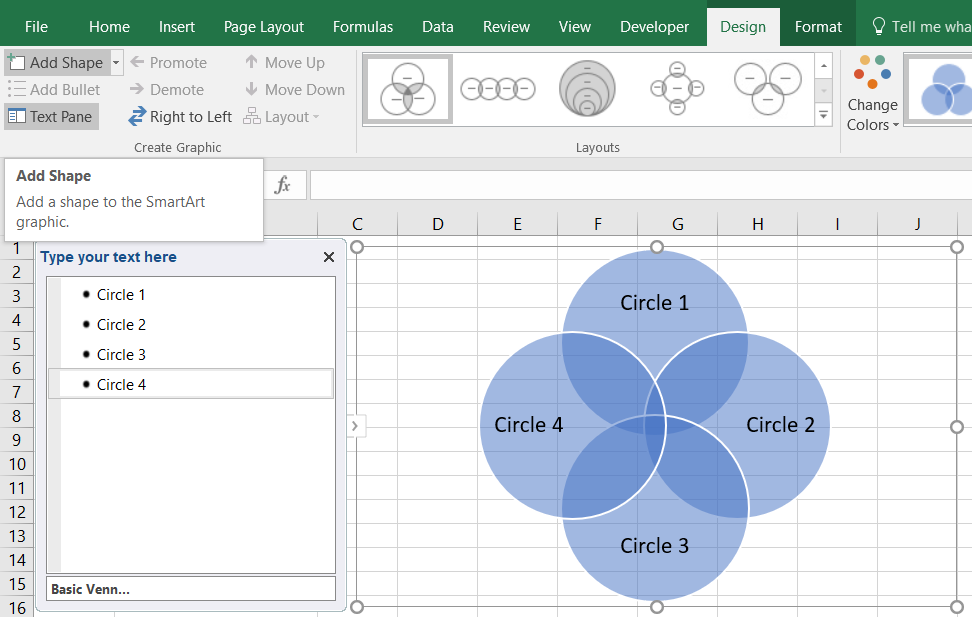
[デザイン] タブの [図形の追加] をクリックします。
-
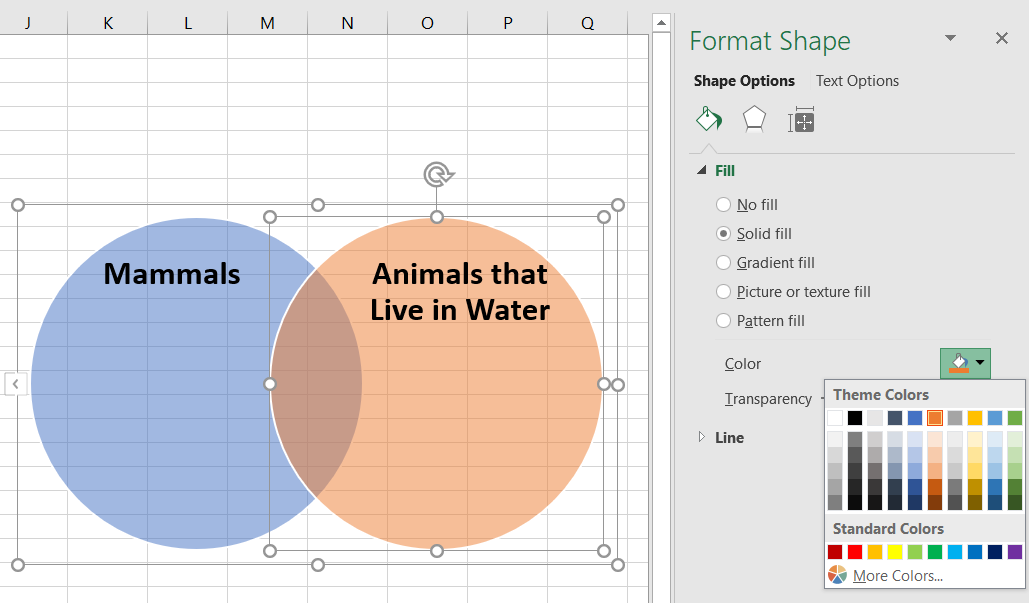
円を削除するには、対象の図形をクリックし、[Delete] キーを押します。ここでは3番目の円を削除し、2つの円にそれぞれ「Mammals (哺乳類)」と「Animals that Live in Water (水中に生息する動物)」のタイトルを追加しています。
- ベン図のスタイルを設定
円のスタイルを設定するには、円のいずれかを右クリックし、[図形の書式設定] を選択します。その後、ウィンドウの右側に表示されるメニューの色を変更します。ここでは、2番目の円の色をオレンジに変更しています。
- 円へのコンテンツの追加
希望通りにベン図のスタイルを設定したところで、円にコンテンツを追加していきます。以下の手順でベン図にテキストを追加します。
-
-
図にテキストを追加するには、円の中にテキストボックスを描画する必要があります。
-
テキストボックスの描画後に、作成済みのリストを使ってボックスに入力していきます (このチュートリアルの初めのステップ2を参照してください)。
-
この例では、「Mammals (哺乳類)」を片側に、「Animals that Live in Water (水中に生息する動物)」を他方に入力しています。哺乳類であり、かつ水中に生息する動物は、図の中心の重複する領域に属します。
-
-
- 対象の円すべてにテキストを追�加し、図を完成させます。
図のスタイルを変更したい場合には、[デザイン] タブに戻り、円の追加や構成の変更をすることができます。ただし、追加したテキストは自動で図形に固定されないため、図の外観が崩れてしまわないよう気をつけましょう。
Lucidchart でベン図を作成
エクセルやパワポ にはない役立つ機能をいくつか備えた Lucidchart ベン図 ツールで、より柔軟に、美しいベン図を作成することができます。自由自在、思いのままに図の書式設定ができ、印象的でプロフェッショナルな外観のベン図を作り上げることが可能です。
以下のシンプルな手順で美しい図を作成できます。
1. 無料で Lucidchart アカウントに登録
こちらをワンクリックしてメールアドレスを入力すれば Lucidchart アカウントの作成ができます。1分もかからず簡単にできます。
2. 図形を追加、またはテンプレートを使用
Lucidchart でベン図を作成する方法はいくつかあります。円をドラッグ・アンド・ドロップして手動で作成することも、組み込みの高度なテンプレートを選んで作成を開始することも可能です。
図形の追加
-
[+ 図形] ボタンをクリックし、ベン図ライブラリを選択します。必ず正しいライブラリを選択するようにしましょう。
-
作図を始める準備ができたら、左側のツールボックスから図形をドラッグしてキャンバスへドロップします。
テンプレートの使用
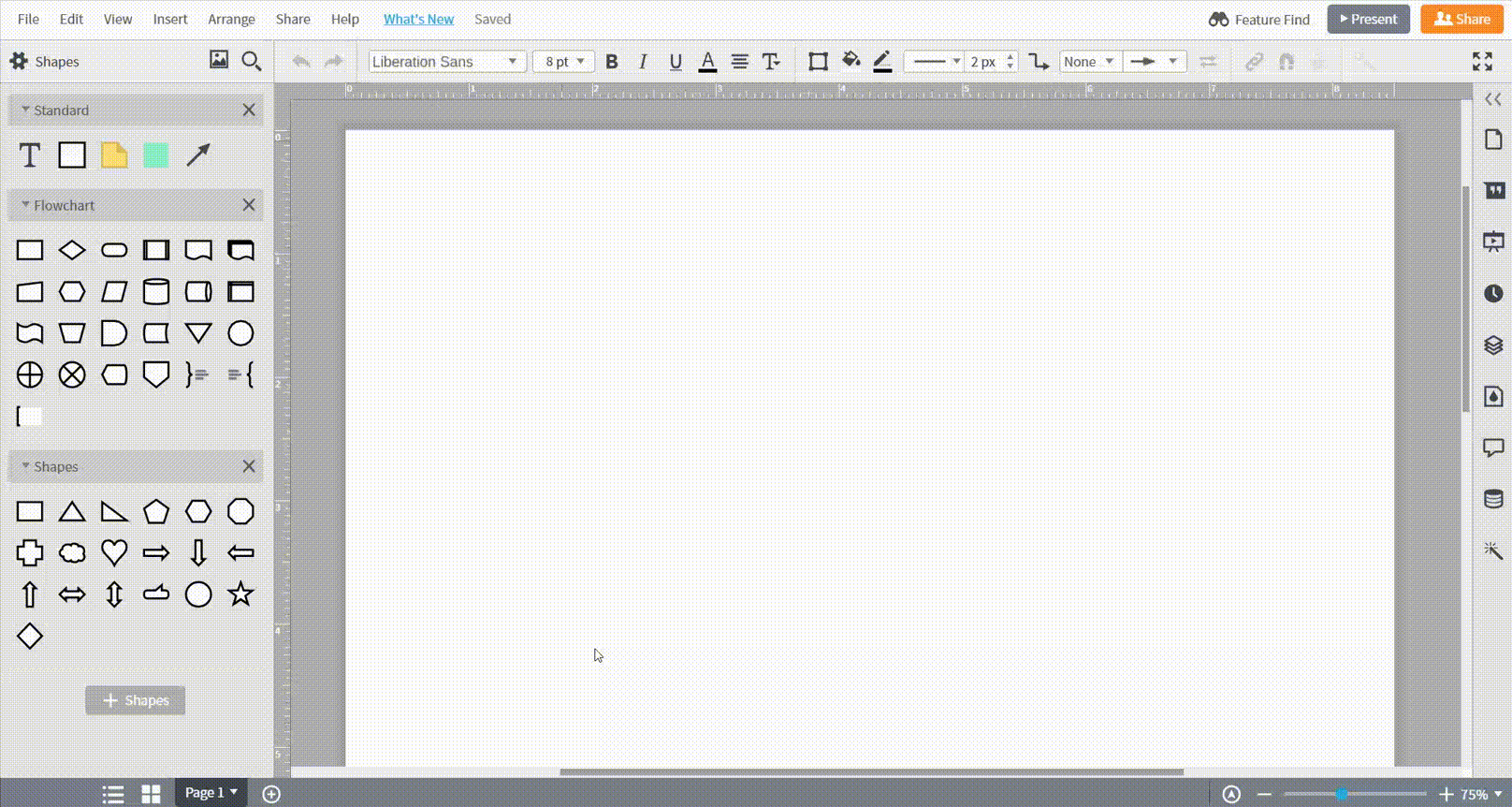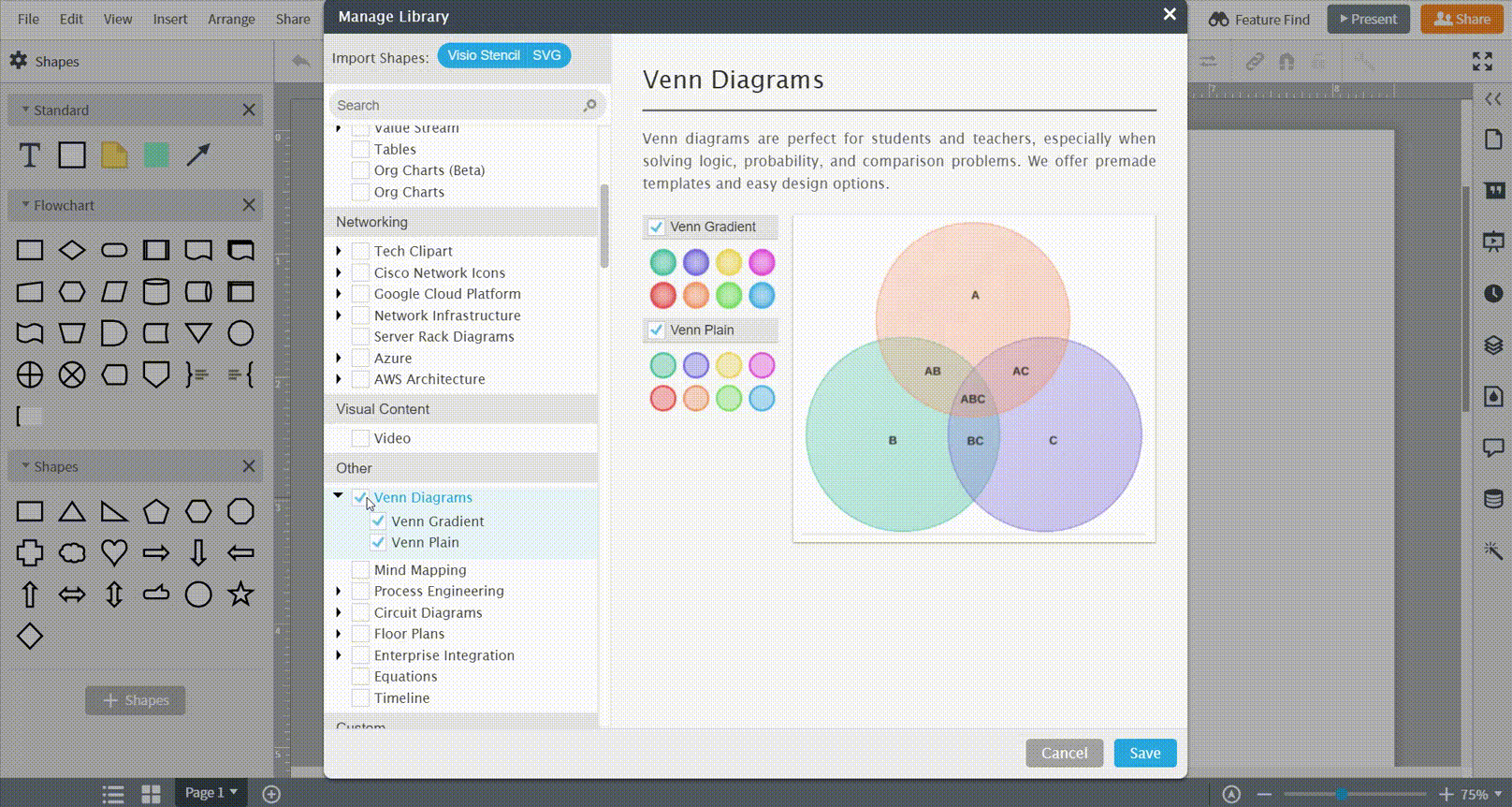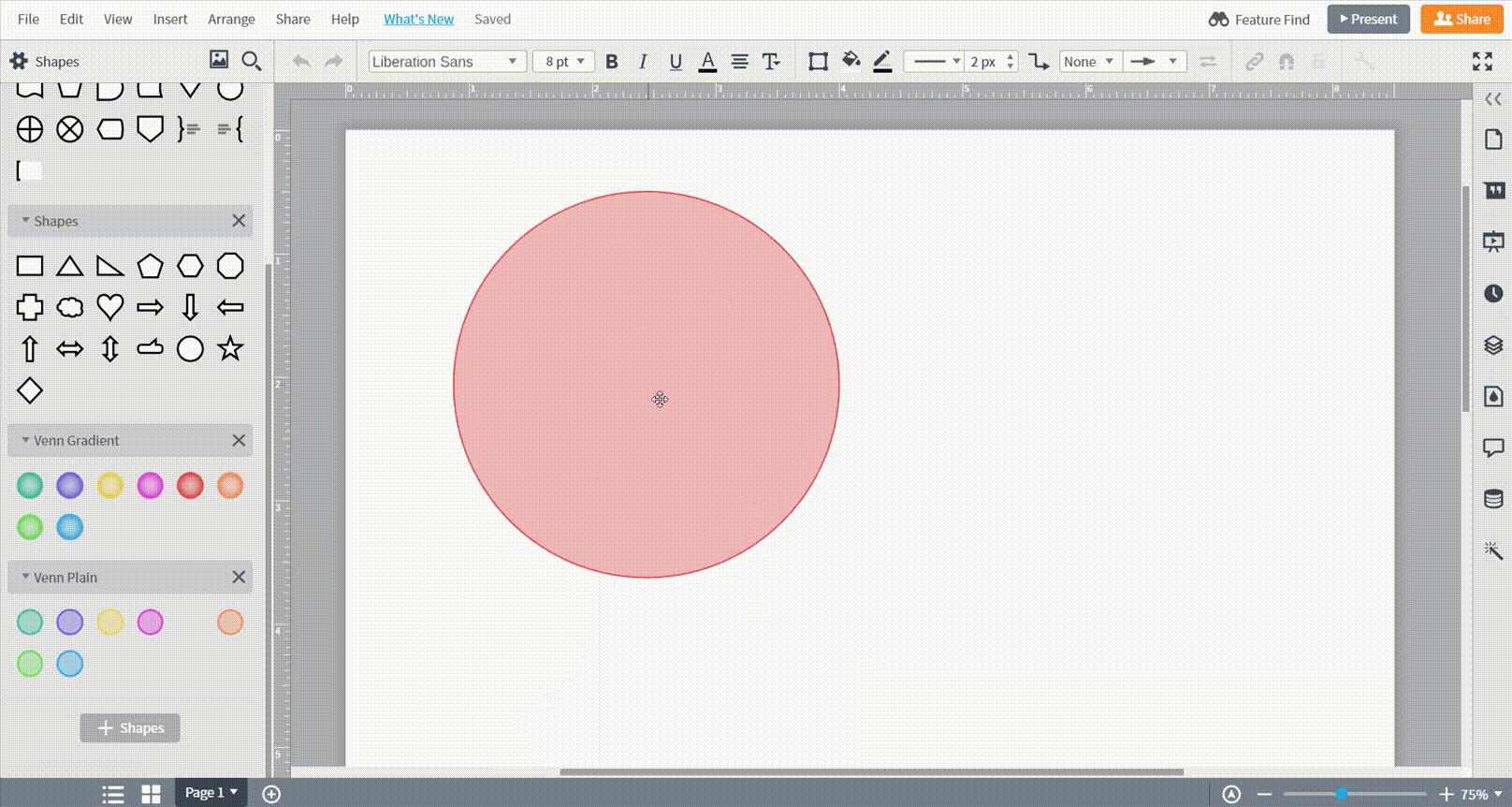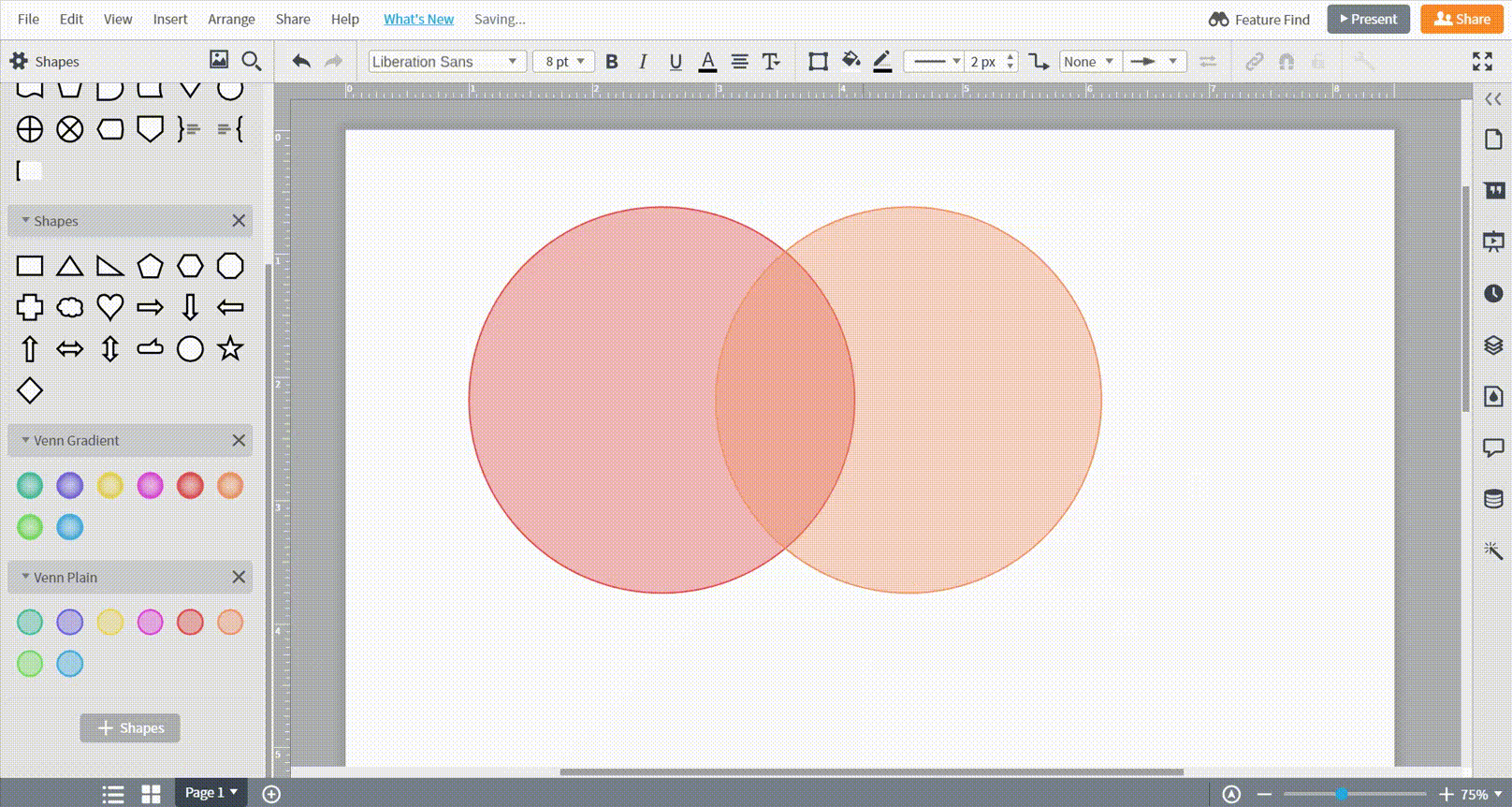
-
Lucidchart ログイン後のホームでオレンジの [+ 文書] ボタンの横の下向き矢印をクリックします。
-
画面右側の [ベン図] テンプレートライブラリをクリックして使いたいテンプレートを選択しましょう!
3. ベン図のスタイルを設定
カスタムの色とスタイルを追加して、ベン図をカスタマイズします。色の変更、境界線の太さやスタイルの変更など、ベン図の要素は通常の図形のように編集することができます。
-
図形を右クリックすると、簡単に編集できます。図形の前後移動、線の描画や図形の切り替えなどのよく使う編集オプションがメニューに表示されます。
-
図形はクリックとドラッグで移動します。縁や角からドラッグするとサイズを変更でき、回転ハンドルアイコンをクリックしてドラッグすると回転することができます。
-
複数の図形を移動するには、[Shift] を長押ししながら��対象の図形それぞれをクリックで選択し、必要に応じてドラッグします。
-
配置やフォントのサイズなどのテキストの変更は、テキストを選択し、ページ上部のプロパティバーからオプションを選択して行います。
-
塗りつぶしの色やグラデーションなどのグラフィック面での変更は、変更したい要素を選択し、ページ上部のプロパティバーからオプションを選択して行います。
パワポでベン図の書き方
1. パワポで新規のプレゼンテーションを開きます。
2. レイアウトを選択してキャンバスをクリーンアップします。[ホーム] > [レイアウト] の順に移動し、白紙のスタイルを選択します。
3. [挿入] タブをクリックし、[SmartArt] を選択します。
パワポでベン図のスタイル設定方法:
- テキストを追加
希望の SmartArt グラフィックを選択すると、ベン図にテキストを追加するよう促すダイアログボックスがポップアップ表示されます。それぞれの円につき、箇条書きのリストのテキストを入力します。

- ベン図のスタイルを設定
ベン図の円のいずれかを右クリックします。[図形の書式設定] を選択します。テキストと図形の書式設定オプションが右側のパネルに表示されます。色を変えてみましょう。ここでは、上の円を赤色に変えています。

- デザインを変更
[デザイン] タブをクリックするだけで、標準のレイアウトをグレードアップすることができます。ここでは、テーマは最初のままとしていますが、黒の背景色に白のテキストと円の枠線、多色の円の3番目のオプションに背景を変更しています。
パワポでデザインしたベン図の完成版はこのようになります。

例えば、ベン図を PPT ファイルではなく PNG 画像として保存したい場合には、[ファイル] > [エクスポート] > [ファイルの種類の変更] の順に選択します。









![[デ�ザイン] タブのリボン](https://d2slcw3kip6qmk.cloudfront.net/marketing/pages/chart/venn-diagram-powerpoint/design-tab.PNG)