Wat is een venn diagram?
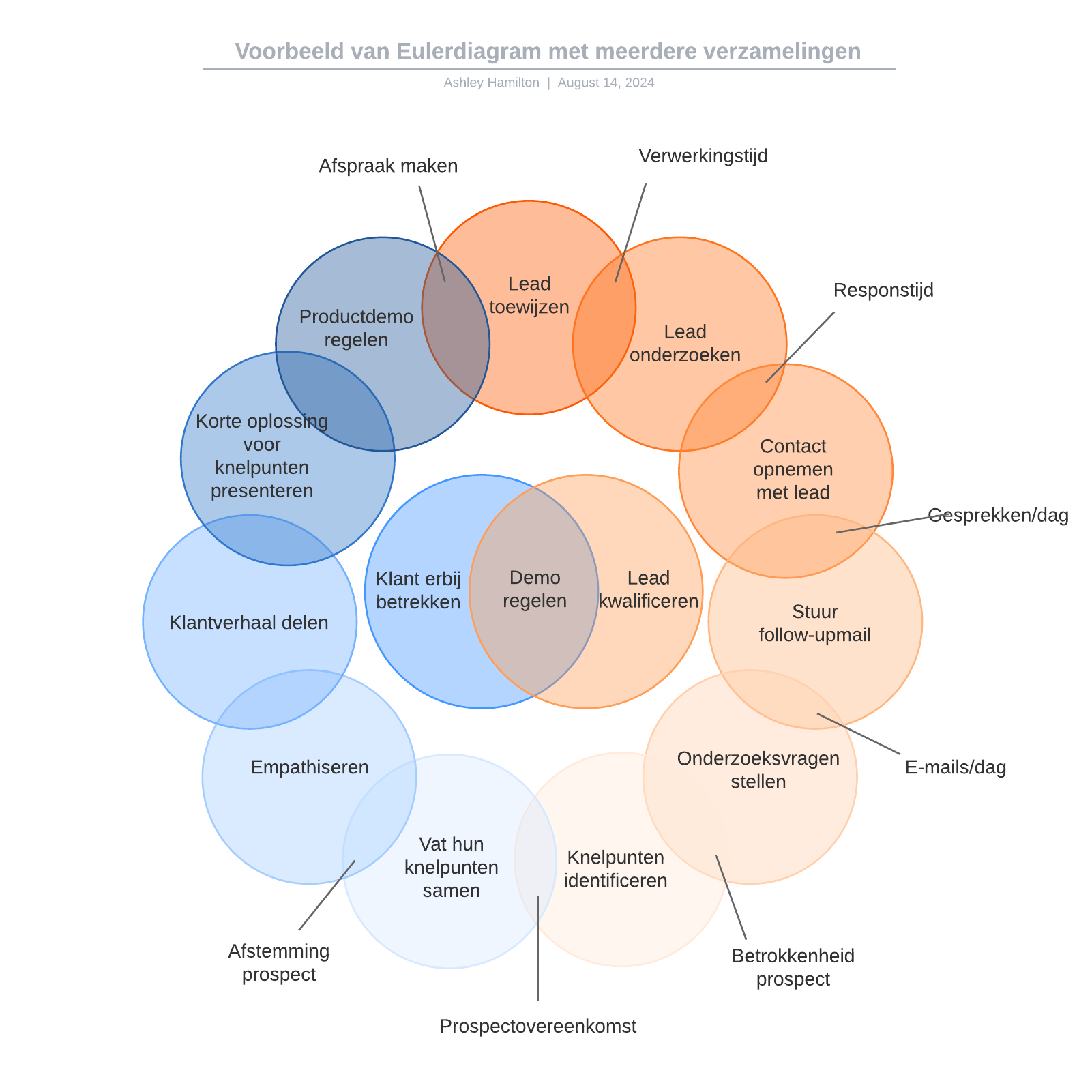
In een venn diagram worden overlappende cirkels of andere vormen gebruikt om de logische relaties tussen twee of meer verzamelingen te illustreren. Vaak worden ze gebruikt om dingen grafisch te organiseren en te illustreren hoe de elementen hetzelfde zijn en verschillend. Venn diagrammen, ook wel verzamelingsdiagrammen of logische diagrammen genoemd, worden veel gebruikt in de wiskunde, statistiek, onderwijs, taalkunde, computerwetenschap en het bedrijfsleven. Veel mensen komen ze voor het eerst tegen op school bij wiskunde of logica; venn diagrammen werden al sinds de jaren 60 veel gebruikt in de "nieuwe wiskunde-curricula". Dit kunnen eenvoudige diagrammen zijn met twee of drie onderdelen van een paar elementen, of behoorlijk verfijnde diagrammen met 3D-presentaties, vooral als het om zes, zeven of zelfs meer sets gaat. Ze worden gebruikt om na te denken over items en weer te geven hoe onderdelen met elkaar verband houden binnen een bepaald "universum" of segment. Met venn diagrammen kunnen gebruikers data visualiseren op een heldere, krachtige manier en ze worden dus veel gebruikt in presentaties en rapporten. Ze zijn nauw verbonden aan Euler-diagrammen, met het verschil dat daarin verzamelingen worden weggelaten als er geen elementen in bestaan. Venn-diagrammen tonen relaties aan zelfs als een verzameling leeg is.



In minder dan 5 minuten aan de slag met Lucidchart
- Gebruik onze online tool om je eerste online diagram te maken op basis van een sjabloon of leeg canvas of importeer een document.
- Voeg tekst, vormen en lijnen toe om je stroomdiagram aan te passen.
- Meer informatie over het aanpassen van de stijl en opmaak in je stroomdiagram.
- Vind wat je nodig hebt met 'Functie zoeken'.
- Deel je stroomdiagram met je team om samen te werken.
Geschiedenis
Venn diagrammen zijn vernoemd naar de Britse logicus John Venn. Hij schreef erover in een artikel uit 1880 genaamd "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings” in het Philosophical Magazine en het Journal of Science.

Maar de oorsprong van dit soort diagrammen ligt veel verder in het verleden, tenminste 600 jaar. Rond 1200 gebruikte de filosoof en logicus Ramon Llull (soms Lull gespeld) uit Mallorca een vergelijkbaar type diagram, dit schreef M.E. Baron in een artikel uit 1969 over de geschiedenis van het diagram. Zij vermeldde ook dat de Duitse wiskundige en filosoof Gottfried Wilhem von Leibnitz vergelijkbare diagrammen tekende aan het eind van de 17e eeuw.


In de 18e eeuw vond de Zwitserse wiskundige Leonard Euler (uit te spreken als Oi-ler) het Euler-diagram uit, de meest directe voorloper van het Venn-diagram. Het was zelfs zo dat John Venn zijn eigen diagrammen Euler-cirkels noemde en geen venn diagrammen. Het woord venn diagram komen we voor het eerst in druk tegen bij de Amerikaanse filosoof Clarence Irving (C.I.) Lewis in zijn boek uit 1918 met de naam A Survey of Symbolic Logic.
vennd iagrammen bleven zich ontwikkelen in de afgelopen 60 jaar met nieuwe ontwikkelingen door de experts David W. Henderson, Peter Hamburger, Jerrold Griggs, Charles E. “Chip” Killian en Carla D. Savage. Hun werk betrof symetrische venn diagrammen en hun relatie met priemgetallen of getallen die niet deelbaar zijn door andere getallen behalve 1 en het getal zelf. Een dergelijk symetrisch diagram, op basis van het priemgetal 7, is algemeen bekend in wiskundekringen als Victoria.
Andere bekende namen in de ontwikkeling van venn diagrammen zijn A.W.F. Edwards, Branko Grunbaum en Henry John Stephen Smith. Zij veranderden onder andere de vormen in de diagrammen zodat eenvoudigere weergave van venn diagrammen mogelijk werd bij grotere aantallen verzamelingen.
Een eenvoudig voorbeeld
Stel dat we het over huisdieren hebben en willen vergelijken over welk huisdier ons gezin het eens kan worden.
In verzameling A vinden we mijn voorkeuren: hond, vogel, hamster.
In verzameling B vinden we de voorkeuren van gezinslid B: hond, kat, vis.
In verzameling C vinden we de voorkeuren van gezinslid C: hond, kat, schildpad, slang.
De doorsnede of intersectie van de drie verzamelingen bevat alleen maar hond. Het ziet er dus naar uit dat we een hond krijgen.
Natuurlijk kunnen venn diagrammen een stuk ingewikkelder worden dan in dit voorbeeld omdat ze uitgebreid worden gebruikt in verschillende vakgebieden.
Doel en voordelen
- Informatie visueel organiseren om de relatie aan te tonen tussen verzamelingen met elementen, zoals wat ze gemeenschappelijk hebben en waarin ze verschillen. Studenten en professionals kunnen ze gebruiken om over de logica van een concept na te denken en de relaties weer te geven voor visuele communicatie. Het kan hierbij gaan om hele elementaire tot zeer geavanceerde zaken.
- Twee of meer keuzes vergelijken om duidelijk te zien wat ze gemeenschappelijk hebben tegenover wat ze verschillend maakt. Dit kan worden gebruikt bij de selectie van een belangrijk product of belangrijke dienst om te kopen.
- Om complexe wiskundige problemen op te lossen. Als u een wiskundige achtergrond heeft uiteraard.
- Om datasets te vergelijken, correlaties te ontdekken en de waarschijnlijkheid dat iets zal gebeuren te voorspellen.
- Om de logica te beredeneren van stellingen of vergelijkingen, zoals de Booleaanse logica achter een trefwoord met gebruik van "of"- en "en"-stellingen en hoe die gegroepeerd zijn.
Gebruik in verschillende vakgebieden
- Wiskunde: venn diagrammen worden veel gebruikt op school om eenvoudige wiskundige concepten te onderwijzen zoals verzamelingen, verenigingen en doorsnedes. Ze worden ook gebruikt in geavanceerde wiskunde om complexe problemen op te lossen en er is uitgebreid over geschreven in wetenschappelijke tijdschriften. Verzamelingenleer is een volledige tak in de wiskunde.
- Statistiek en kansberekening: Statistici gebruiken venn diagrammen om te voorspellen hoe waarschijnlijk het is dat iets zich voordoet. Hierbij hoort ook bijvoorbeeld predictive analytics. Verschillende dataverzamelingen kunnen worden vergeleken om de mate van overeenkomst en verschil te vinden.
- Logica: Venn diagrammen worden gebruikt om de validiteit te bepalen van bepaalde argumenten en conclusies. In deductie wordt gesteld dat als de vooronderstellingen waar zijn en de argumentvorm juist is, dan moet de gevolgtrekking waar zijn. Bijvoorbeeld als alle honden dieren zijn en ons huisdier Mojo een hond is, dan moet Mojo een dier zijn. Als we variabelen toewijzen dan kunnen we stellen dat honden C zijn, dieren zijn A en Mojo is B. Als argumentvorm zeggen we: Alle C zijn A. B is C. Daarom is B een A. Een diagram dat hiermee verband houdt in de logica is een waarheidstabel, waarin de variabelen in kolommen worden geplaatst om te beslissen wat logisch juist is. Een ander verwant diagram is het Randolph-diagram of R-diagram, naar de wiskundige John F. Randolph. Hierin worden regels gebruikt om verzamelingen te definiëren.
- Taalkunde: Venn diagrammen worden gebruikt om de overeenkomsten en verschillen tussen talen te onderzoeken.
- Begrijpend leren lezen: Docenten kunnen venn diagrammen gebruiken om de leesvaardigheid van hun leerlingen te vergroten. Leerlingen kunnen diagrammen tekenen om ideeën waar ze over lezen te vergelijken en onderscheiden.
- Computerwetenschap: Programmeurs gebruiken venn diagrammen om computertalen en hiërarchieën te visualiseren.
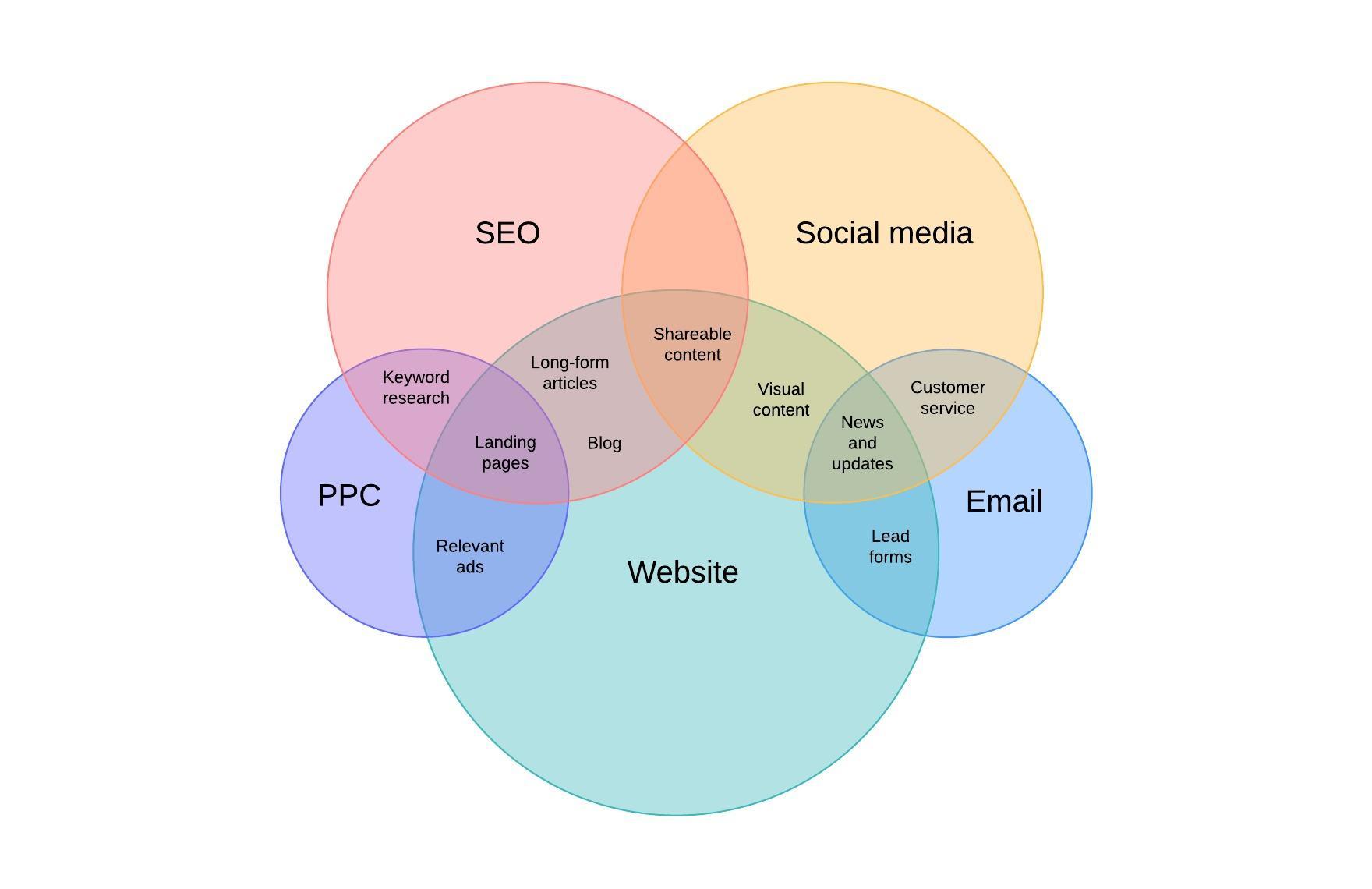
- Handel: Venn diagrammen worden gebruikt om producten, diensten, processen en eigenlijk alles dat in een verzameling gevat kan worden te vergelijken en onderscheiden. En ze zijn een effectief communicatiemiddel om die vergelijking te illustreren.
Woordenlijst venn diagram
| Verzameling | Een verzameling van dingen. Gezien hoe divers het gebruik van venn diagrammen is, kunnen die dingen echt van alles zijn. De dingen kunnen elementen, objecten, leden of iets vergelijkbaars genoemd worden. |  |
| Vereniging | Alle elementen in de verzamelingen. |  |
| Snijpunt | De objecten die gemeenschappelijk zijn in de verzamelingen. Soms een subset genaamd. |  |
| Symmetrisch verschil van twee verzamelingen | Alles behalve de doorsnede. |  |
| Absolute complement | Alles dat zich niet in de verzameling bevindt. |  |
| Relatief complement | In de ene verzameling maar niet in de andere. |  |
| Venndiagram op schaal | Ook wel een proportioneel gebied genoemd. De cirkels (of andere vormen) krijgen de grootte van hun proportionele vertegenwoordiging in het geheel. |  |
| Reuleaux-driehoek | Vorm gemodelleerd uit de doorsnede van drie cirkels of vormen zoals in een venndiagram. |  |
| Verzameling-notaties |
De concepten die geïllustreerd worden in venndiagrammen worden weergegeven door middel van wiskundige notaties zoals die voor verzamelingen en deelverzamelingen (tussen haakjes), verenigingen (met een u-achtig symbool) en doorsneden (met een omgekeerd u-symbool) | |
| Verzamelingenleer | Het deelgebied van wiskunde betreffende verzamelingen. |
Je venn diagram opmaken in PowerPoint
Tekst toevoegen
Als je de gewenste SmartArt-afbeelding hebt geselecteerd, verschijnt er een dialoogvenster waarin je tekst aan je venn diagram kunt toevoegen. Vul de tekstvelden in voor elke cirkel in de lijst.

De stijl van je venn diagram wijzigen
Klik met de rechtermuisknop op een van de cirkels in je venn diagram. Klik op Vorm opmaken. Aan de rechterkant verschijnt nu een paneel met opmaakopties voor zowel de tekst als de vorm. Verander bijvoorbeeld de kleur - wij hebben de bovenste cirkel rood gemaakt.

Het ontwerp wijzigen
Om de standaardindeling een beetje op te leuken, klik je op het tabblad Ontwerpen. In dit voorbeeld hebben we het eerste thema behouden, maar de achtergrond veranderd in de derde variant met een zwarte achtergrond, witte tekst en contouren, en andere tinten voor de cirkels.
Het in PowerPoint ontworpen venn diagram ziet er uiteindelijk zo uit:

Stel nu dat je je venn diagram niet als PPT-bestand, maar als PNG-afbeelding wilt opslaan. Hiervoor ga je naar Bestand > Exporteren > Bestandstype wijzigen.
Leuk om te weten: venn diagrammen op tv
Er zijn niet veel diagrammen die bekend zijn geworden in de populaire cultuur, maar het venn diagram wel.
- TV-serie: In de CBS-serie NUMB3RS, die werd geproduceerd van 2005 tot 2010, gebruikt wiskundig genie Charles Eppes een venn diagram om te bepalen welke verdachten voldoen aan een beschrijving en een gewelddadig verleden hebben.
- Comedy: In Late Night with Seth Meyers van NBC is een terugkerend item dat “Venn Diagrams” heet, hierin worden twee schijnbaar ongerelateerde items vergeleken om de overeenkomsten te ontdekken (hoopt hij).
Stappen om een eenvoudig venn diagram te tekenen en gebruiken
- Bepaal het doel. Wat wil je vergelijken en waarom? Dit helpt om de verzamelingen te bepalen.
- Brainstorm over de elementen in je verzamelingen, ofwel op papier of met een platform zoals Lucidchart.
- Gebruik nu je diagram om de verzamelingen te vergelijken en onderscheiden. Je ziet dan wellicht dingen in een ander licht en kunt observaties, keuzes, argumenten of beslissingen maken.
Een venn diagram maken in PowerPoint
1. Open een nieuwe presentatie in PowerPoint.
2. Maak je canvas leeg door de indeling te wijzigen. Ga onder Start naar Indeling en kies de lege presentatie.
3. Klik op het tabblad Invoegen en selecteer SmartArt.
Een venn diagram maken in Lucidchart
Lucidchart heeft verschillende handige functies die je in PowerPoint niet zult vinden en biedt daardoor veel meer flexibiliteit om een mooi venn diagram te maken. Omdat je alles naar hartenlust kunt aanpassen, is Lucidchart een ideale tool voor het maken van schitterende, professioneel ogende venn diagrammen.
Met deze eenvoudige stappen kun je fantastische diagrammen maken:
1. Meld je aan voor een gratis Lucidchart-account
Je bent slechts een klik en een e-mailadres verwijderd van een nieuw account bij Lucidchart. Klik hier, dan ben je binnen een minuutje klaar.
2. Voeg vormen toe of gebruik een sjabloon
In Lucidchart zijn er een aantal manieren om een venn diagram te maken. Je kunt cirkels verslepen om er handmatig een te bouwen, of je kunt een van onze handige sjablonen als basis gebruiken.
Vormen toevoegen
-
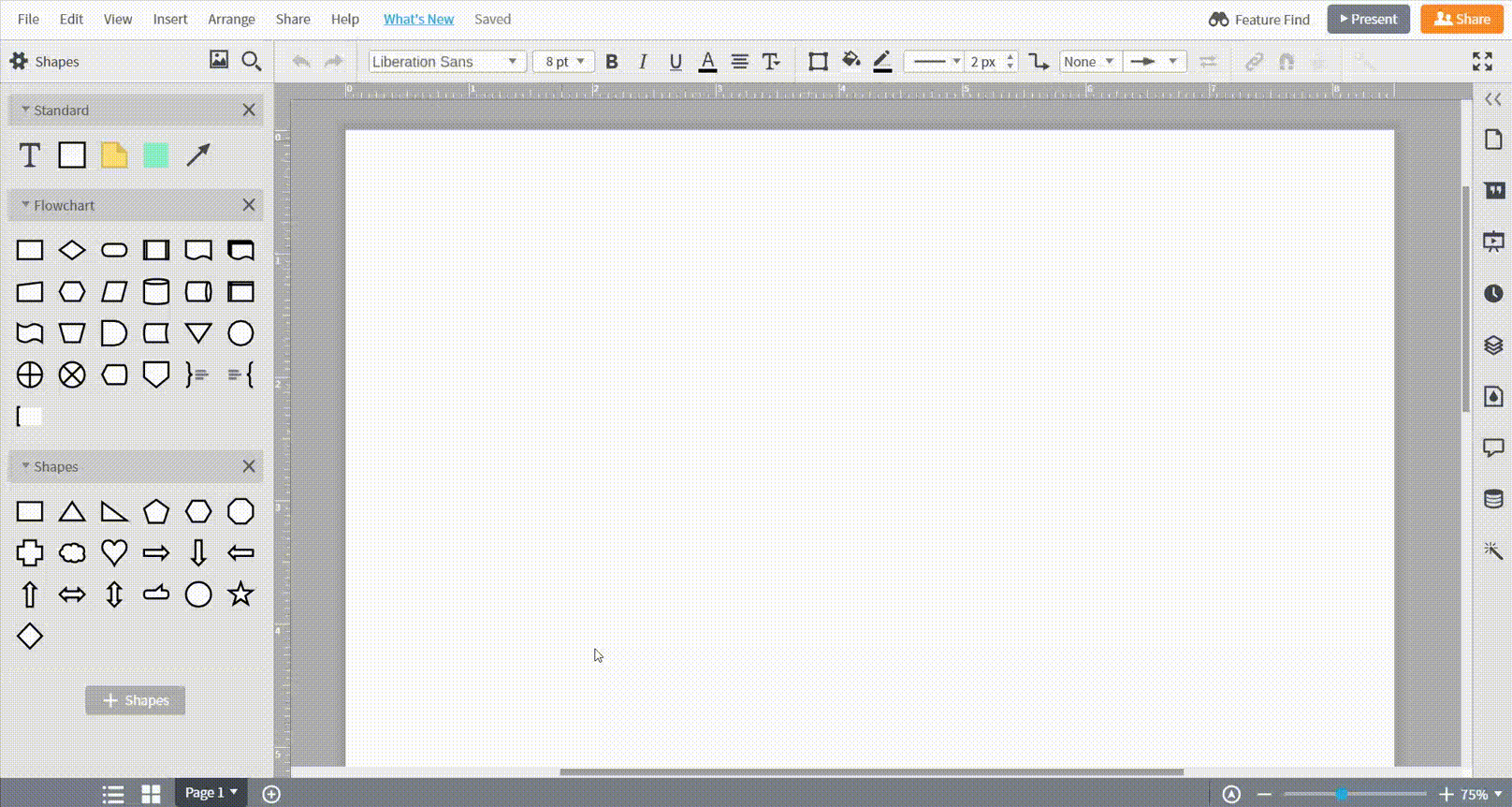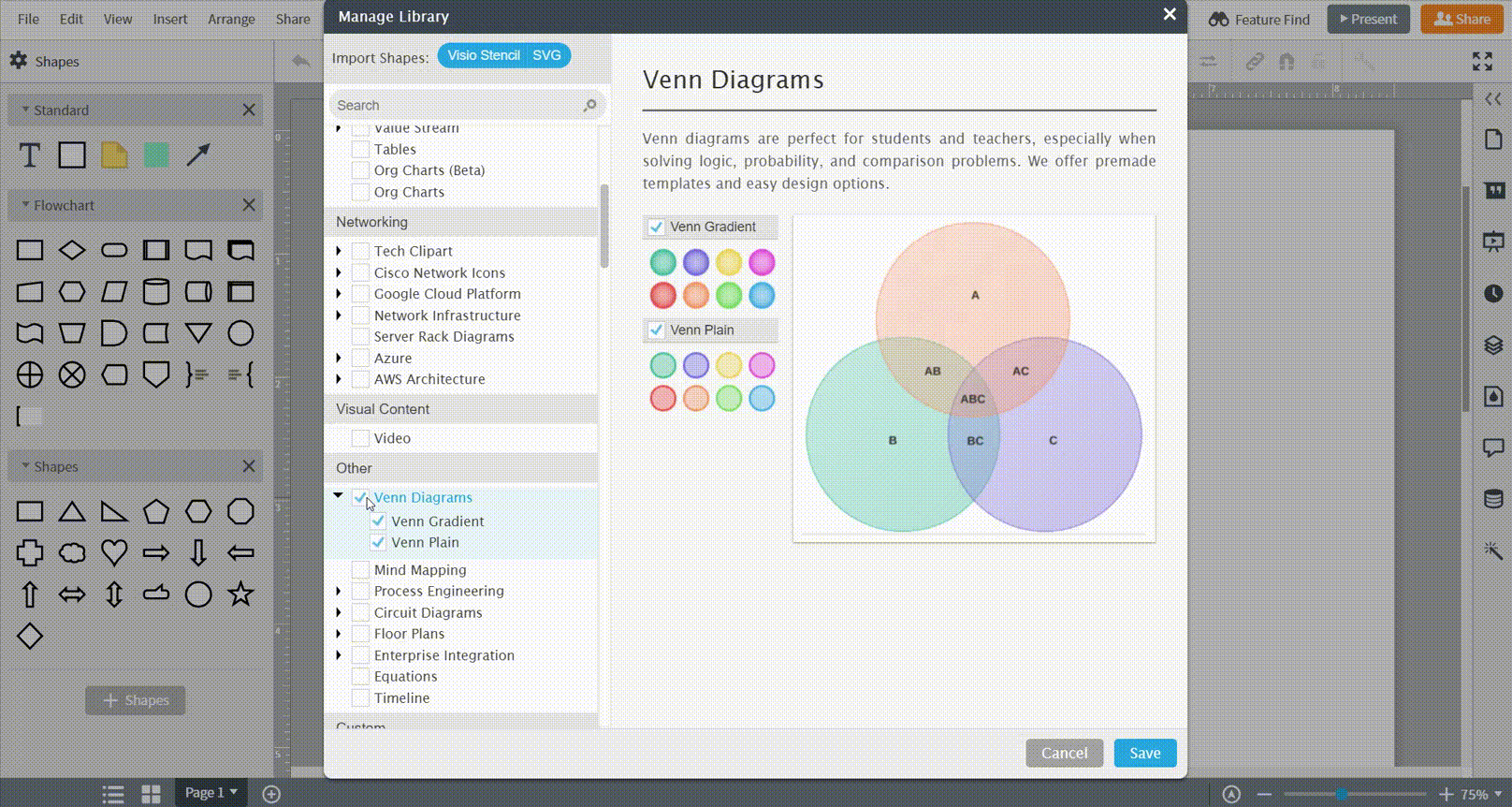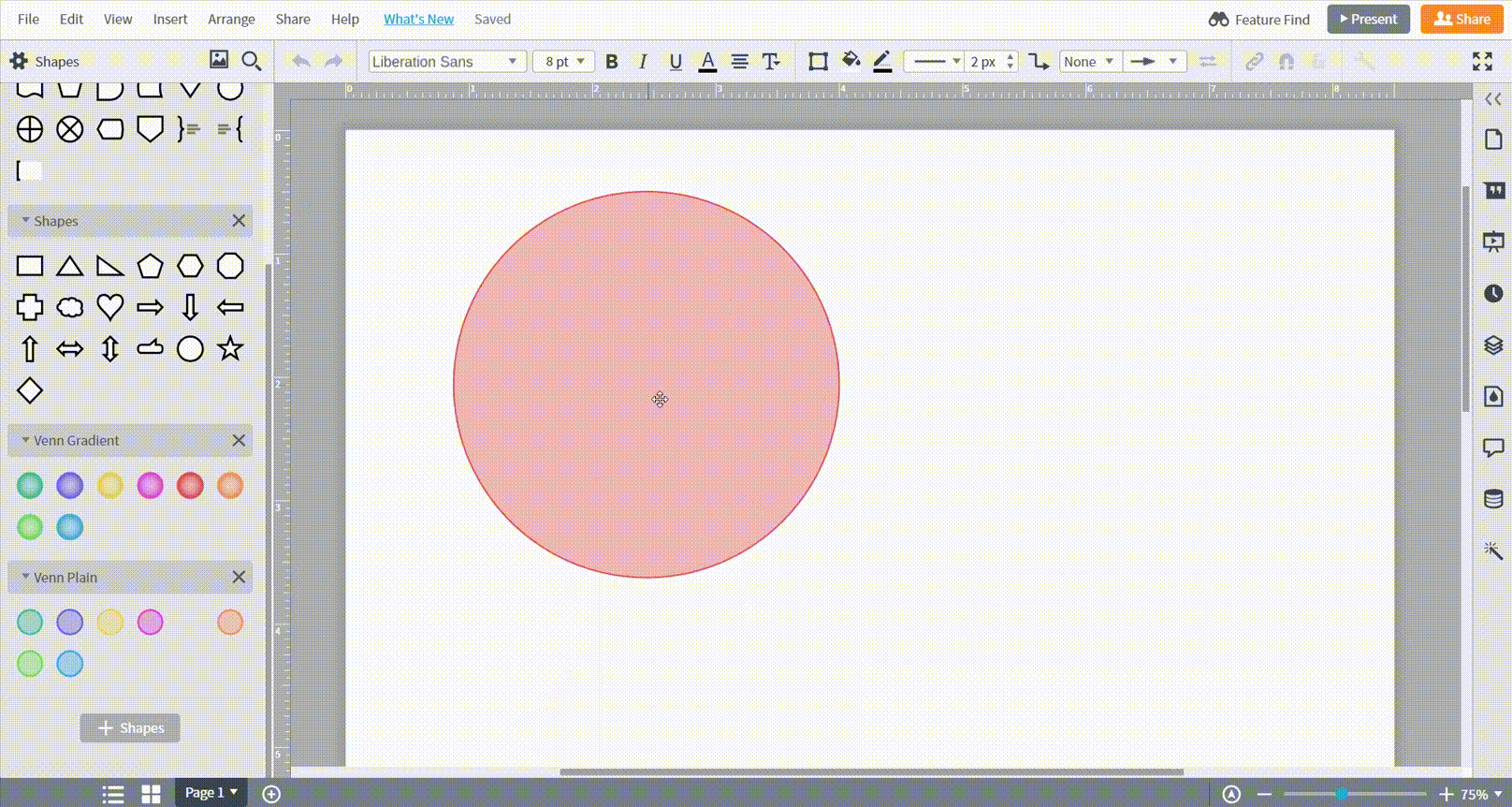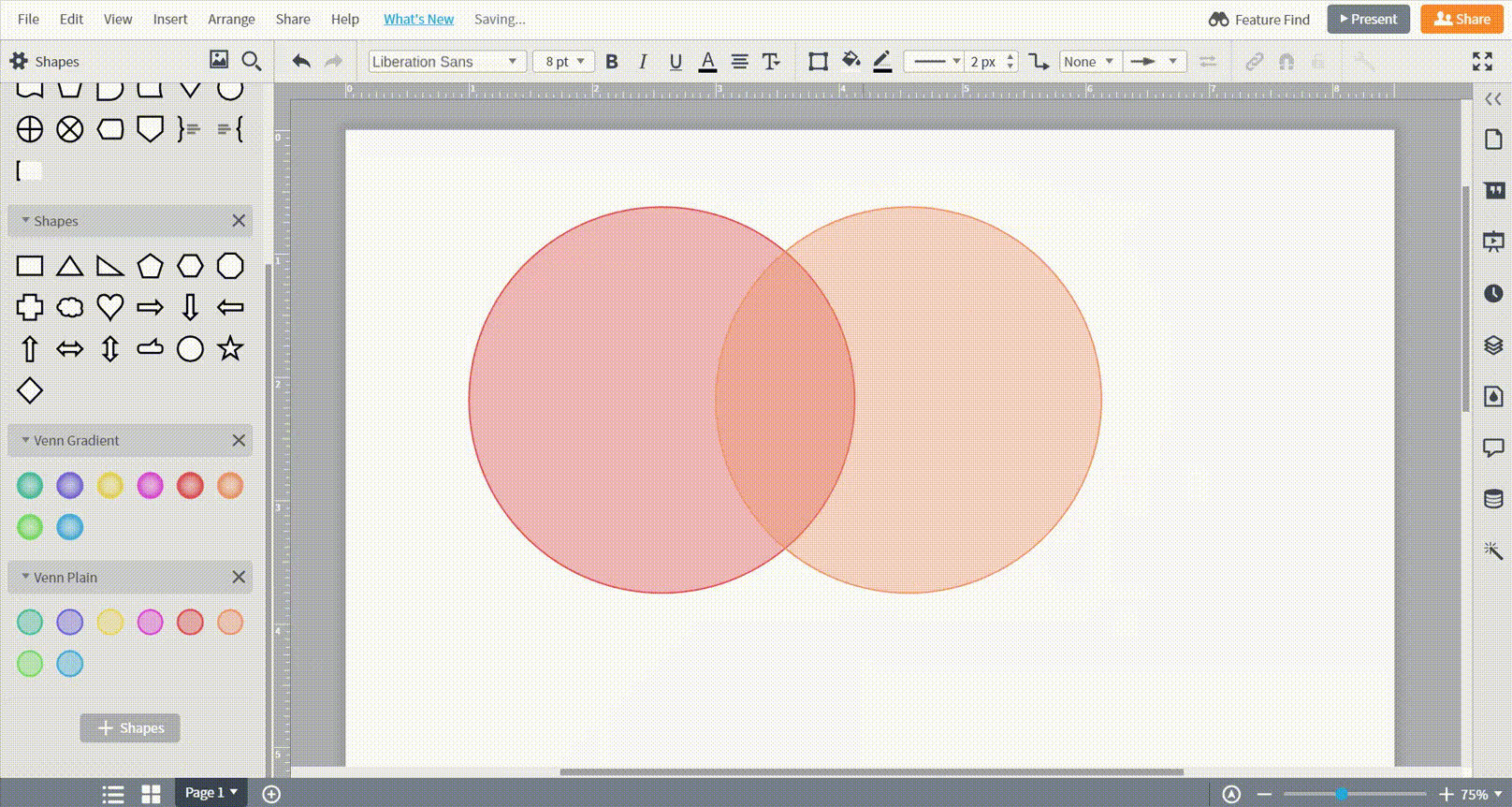
Zorg ervoor dat je de correcte vormbibliotheken open hebt staan door op de knop '+ Vormen' te klikken en de bibliotheken voor venn diagrammen te selecteren.
-
Als je klaar bent om te beginnen, sleep je een vorm uit de toolbox aan de linkerkant en zet je de vorm neer op het canvas.
Een sjabloon gebruiken
-
Klik in de Documentwachtrij van Lucidchart op de pijl omlaag naast de oranje knop met '+ Document'.
-
Klik aan de rechterkant van het scherm op de sjablonenbibliotheek voor venn diagrammen en kies de sjabloon die jij wilt gebruiken!
3. Wijzig de stijl van je venn diagram
Geef je venn diagram een persoonlijk tintje met aangepaste kleuren en stijlen. Je kunt de elementen van je venn diagram net als gewone vormen bewerken door bijvoorbeeld de kleuren, randstijl en randdikte aan te passen.
-
Voor snelle bewerkingen kun je een vorm aanklikken met de rechtermuisknop. Er verschijnt dan een menu met veelgebruikte bewerkingsopties, zoals een item naar de voor- of achtergrond verplaatsen, een lijn trekken of de vorm veranderen.
-
Om een vorm te verplaatsen kunt u deze aanklikken en verslepen. Sleep vanaf een rand of hoek om de grootte te wijzigen, klik op het handvat-icoon en sleep het om de vorm te roteren.
-
Om meerdere vormen te verplaatsen, kun je ze selecteren door elk object aan te klikken terwijl je Shift ingedrukt houdt. Vervolgens kun je ze naar de gewenste positie slepen.
-
Om tekst aan te passen, inclusief uitlijning en lettergrootte, selecteer je de tekst en kies je uit de opties in de balk Eigenschappen bovenaan de pagina.
-
Om grafische kwaliteiten zoals vulkleur en kleurovergangen te wijzigen, selecteer je het element dat je wilt aanpassen en kies je uit de opties in de eigenschappenbalk bovenaan de pagina.