決定木分析
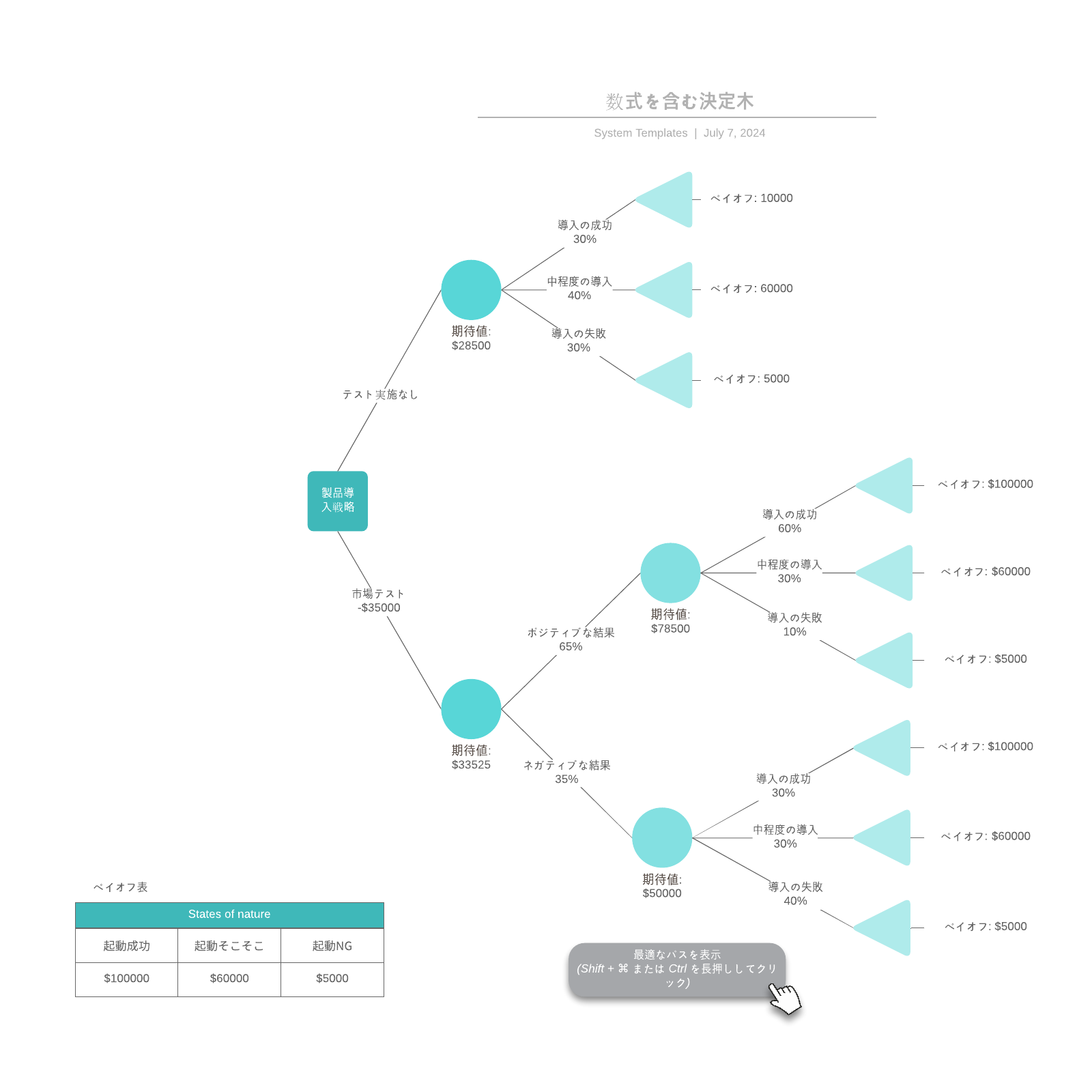
(デシジョンツリー)
とは？

決定木分析は英語では（Decision Tree・デシジョンツリー)と呼ばれており、一連の関連する選択の想定しうる結果を可視化させた分析です。個人や組織が、コスト、可能性や利点を比較して取りうるアクションを評価する上で有用な図です。非公式な議論を促進したり、数学的に最善の選択を計算するアルゴリズムを図式化したり、さまざまな用途に利用できます。

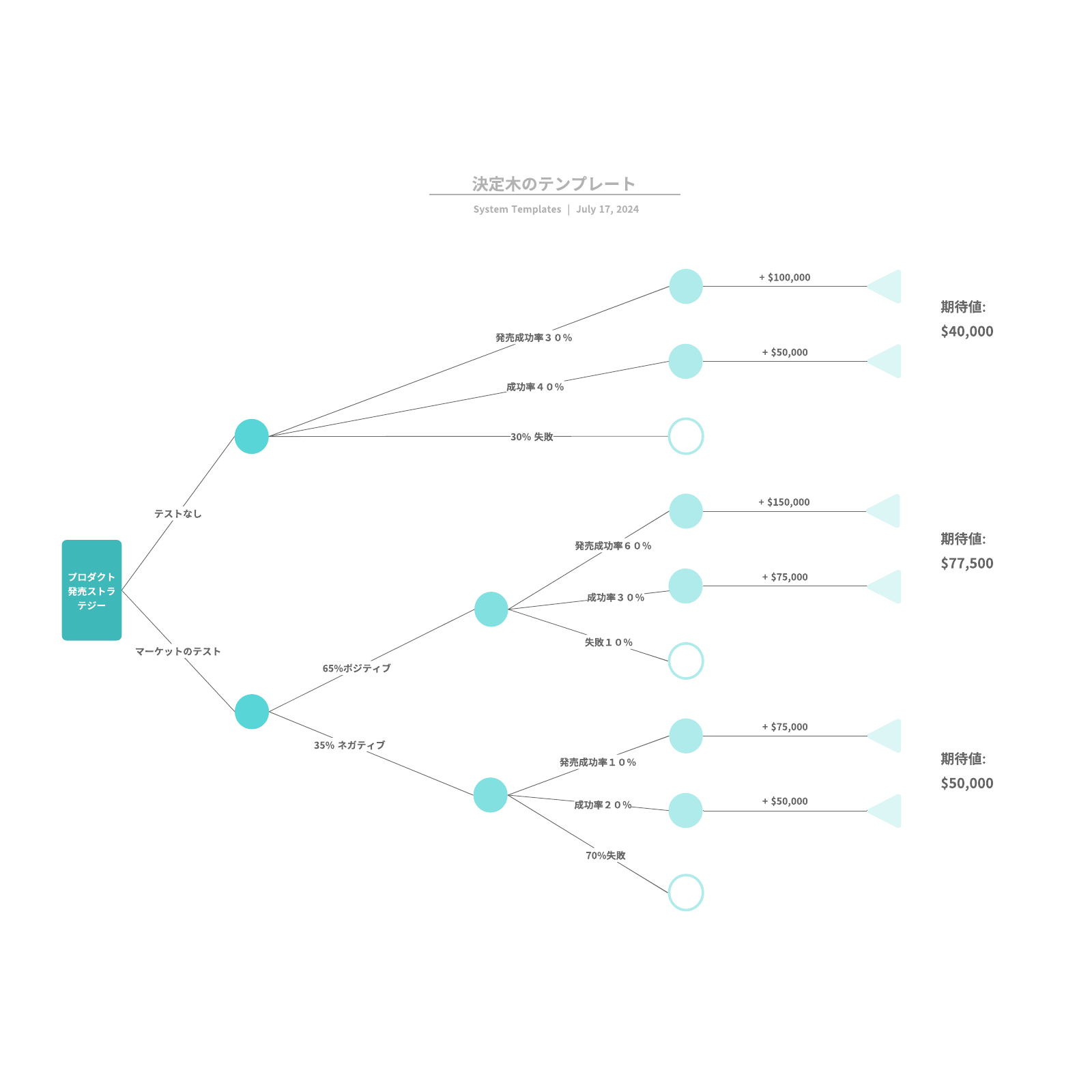
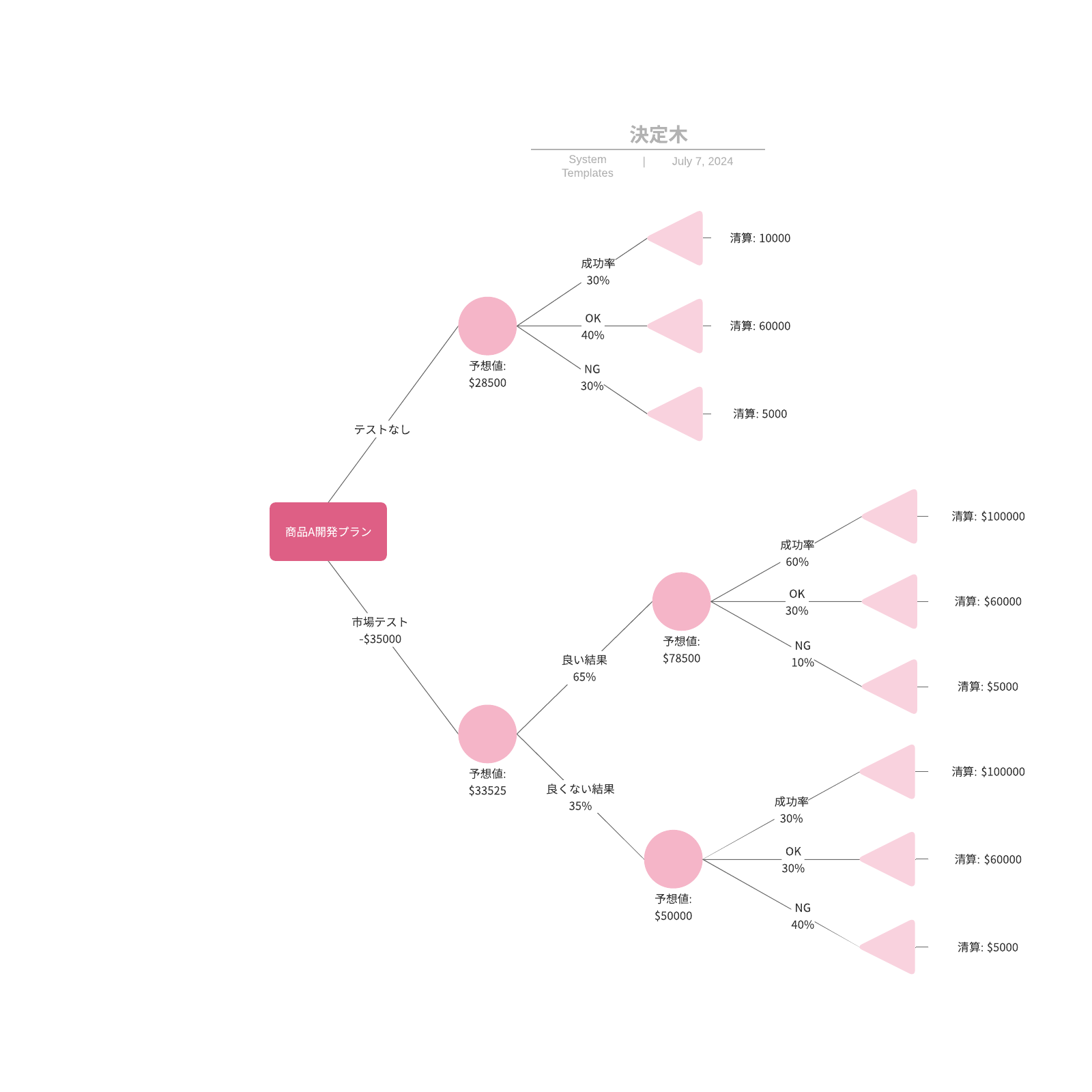
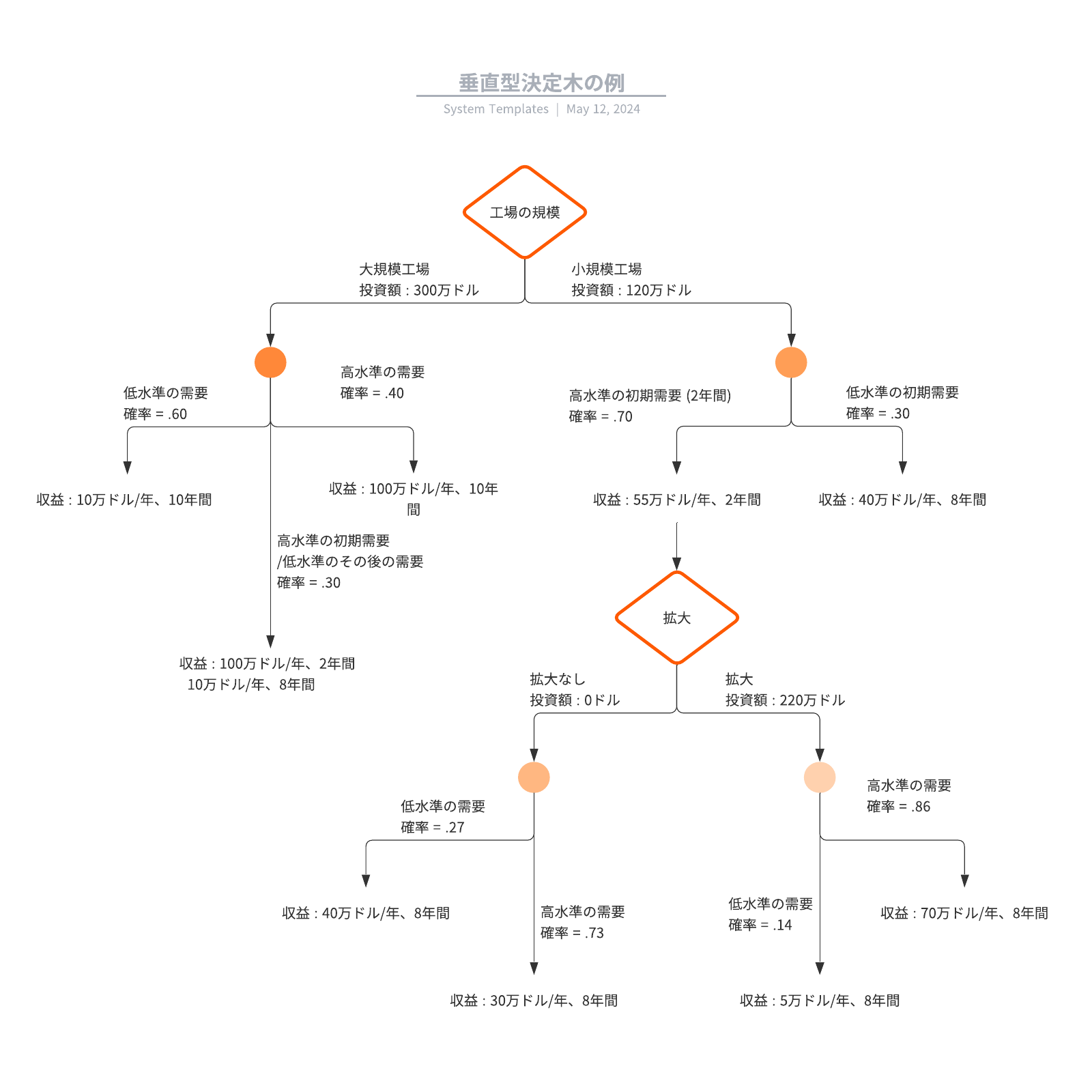
決定木は通常、1つのノードから始まり、想定しうる結果へと分岐していきます。これらの結果はそれぞれ、他の可能性へと分岐する追加のノードへとつながります。結果として、木のような形が形成されます。

ノードには、確率ノード、決定ノードと終了ノードの3種類があります。確率ノードは丸で示され、特定の結果の可能性を表します。正方形で示される決定ノードはすべき決定を表し、終了ノードは決定のパスの最終的な結果を示します。

多くの人に馴染みがあり、比較的わかりやすいフローチャート記号で決定木を作成することも可能です。

覚えておきたい決定木の種類

• 分類木
• 回帰木
• アンサンブル学習
• ランダムフォレスト

 

このセクションでは、決定木分析を正しく可視化させる作り方ステップをご紹介しています。

1. 主となる決定から始めます。この点を示す小さなボックスを描画し、ボックスから右側へ線を引いて考えうる解決策やアクションへとつなげます。適宜ラベルを付けます。

2. 確率ノードと決定ノードを追加し、以下のように木を展開していきます。

• 決定がもう1つ必要な場合には、ボックスを追加します。
• 結果が不明確な場合には、丸を描画します (丸は確率ノードを表します)。
• 問題が解決した場合には、(とりあえず) 空白のままとします。

各決定ノードから想定しうる解決策を描き、各確率ノードからは想定しうる結果を示す線を描きます。選択肢を数値的に分析する場合には、各結果の確率と各アクションの費用も含めます。

3. それぞれの線が終点に到達するまで展開を続けます。終点とは、すべき選択や考慮すべき結果がなくなった点を指します。その後、想定しうる結果のそれぞれに値を割り当てます。値としては、抽象的なスコアやまたは金融資産の価値などが考えられます。終点を示す三角形を追加します。

このステップだけで、決定木が完成し、すべき決定について分析する準備が整いました。

木に含まれるそれぞれの選択に期待する効用や値を計算することで、リスクを最小化し、望ましい結果に到達する可能性を最大化することができます。

ある選択に期待する効用を計算するには、対象の決定で期待される利点からそれに要する費用を差し引きます。期待される利点は、対象の選択に起因しうるすべての結果に対して発生確率を乗算した値の合計値に等しくなります。ここでは、上記の例についてこれらの値を算出しています。

どの結果が最善であるかを識別するには、意思決定者の選好する効用を考慮に入れることが重要です。低リスクのオプションを選好する人もいれば、ハイリスク・ハイリターンを望む人もいるでしょう。

決定木と確率モデルを併用する場合には、モデルを使ってあるイベントの条件付き確率、また他のイベントが発生すると仮定した場合のそのイベントの発生確率を算出することもできます。これを算出するには、最初のイベントから図を開始し、そこから対象のイベントへとパスをつなげていきます。その過程で各イベントに確率を乗算していきます。

こうすることで、決定木を従来型のツリー図のように使い、2回コイントスをする場合など、特定のイベントの確率を描き出すことができます。

このセクションでは、決定木の長所と短所について説明しています。

• 決定木は理解しやすい
• 具体的なデータの有無にかかわらず利用でき、データの準備が最小限で済む
• 既存の木（ツリー）に新しいオプションを追加できる
• いくつかの選択肢から最善のものが選べる
• 他の意志決定支援ツールと組み合わせやすい

ただ、時には決定木分析が複雑になりすぎることもあります。こうした場合は、よりコンパクトな影響図の方が適しているでしょう。影響図は、重要な決定、入力と目標に焦点を絞ったものです。

機械学習、データマイニングや統計などに応用する自動予測モデルの構築に決定木を役立てることもできます。決定木学習と呼ばれるもので、ある項目に関する観察を考慮してその項目の値の予測を行う方法です。

これらの決定木では、ノードは決定ではなく、データを表します。分類ツリーとも呼ばれる種類のもので、各分岐には一連の属性または分類ルールが含まれます。これらは、その線の終端に配置される特定の分類ラベルと関連付けられます。

これらのルールは決定ルールとも呼ばれ、「条件1、条件2および条件3が満たされた場合、 y の確率で結果が x となる」というように、各決定またはデータの値で構成される if-then 節で表現することができます。

データを追加することで、値の有限集合のうちどれに対象物が属するかをモデルがより正確に予測できるようになります。その後、この情報をより大規模な意思決定モデルへの入力として利用することができます。

予測変数は、価格などの実数となることもあります。継続的で無限の想定しうる結果を用いた決定木は、回帰木と呼ばれます。

精度を高めるため、以下の方法で複数の木を組み合わせて使うこともあります。

• バギング - ソースデータをリサンプリングして複数の木を作成し、その後これらの木に投票をさせてコンセンサスを導出します。
• ランダムフォレスト分類器 - 分類率を高めるため、複数の木で構成されます。
• ブーステッドツリー - 回帰木と分類木に使用できます。
• ローテーションフォレスト - これに含まれる木はすべて、ランダムなデータの一部への PCA (主成分分析) を使って処理されています。

レベルや質問の数が最小限で、最大限のデータを表示できている図の状態が、決定木として最適なものとされています。最適化された決定木作成のためのアルゴリズムには、CART、ASSISTANT、CLS や ID3/4/5などがあります。ターゲット変数を右側に配置し、相関ルールを構築する方法で決定木を作成することもできます。

いずれの方法でも、各レベルでデータを分割する最善の方法を判断する必要があります。判断の方法としては、ジニ不純度、情報ゲインや分散減少を測定するものが一般的です。

機械学習への決定木の応用には以下の利点があります。

• データ予測への木の使用コストがデータポイントの追加ごとに低減する
• カテゴリーデータと数値データ双方について使用できる
• 複数の出力をもつ問題のモデル化ができる
• ホワイトボックスモデルを使用することで結果が説明しやすくなる
• 木の信頼性をテストおよび定量化できる
• ソースデータの前提条件違反の有無にかかわらず精度が保たれる傾向にある

その反面で、以下のような欠点もあります。

• 複数のレベルを含むカテゴリーデータに応用する場合に、情報ゲインはレベル数の最も多い属性に対して有利となる
• 不確実性やリンクされた結果が多い場合の計算が複雑となる可能性がある
• 決定グラフでは OR によるノード接続が可能であるのに対し、ノード間の接続が AND に限定される