It’s time to have a serious talk about Venn diagrams—and we're not talking about the Venn diagrams from your grade-school days. We’re talking about the hardcore visuals produced by serious professionals to represent complex mathematical ideas.

Venn diagrams are visual representations of mathematical sets—or collections of numbers or things—that are studied using a branch of logic called set theory. Set theory is one of the foundational systems for mathematics, and it helped to develop our modern understanding of infinity and real numbers.

Researchers and mathematicians have developed a language and system of notation around set theory. If you want to get in on their secrets, you'll want to become familiar with these Venn diagram symbols.

This guide will walk you through the process of making a Venn diagram, explaining the symbols along the way. We’ll be using Lucidchart to build our examples because it’s easy to use and completely free. If you would like to follow along or build your own Venn diagram, all you have to do is create a free account. Now let’s get to it!

Venn diagrams and set theory

There are more than 30 symbols used in set theory, but only three you need to know to understand the basics. Once you’ve mastered these, feel free to move on to the more complicated stuff.

Union of two sets: ∪

Each circle or ellipse represents a category. The union of two sets is represented by ∪. (Don't confuse this symbol with the letter “u.”)

This is a two-circle Venn diagram. The green circle is A, and the blue circle is B. The complete Venn diagram represents the union of A and B, or A ∪ B. Feel free to click on the image to try this diagram as a template.

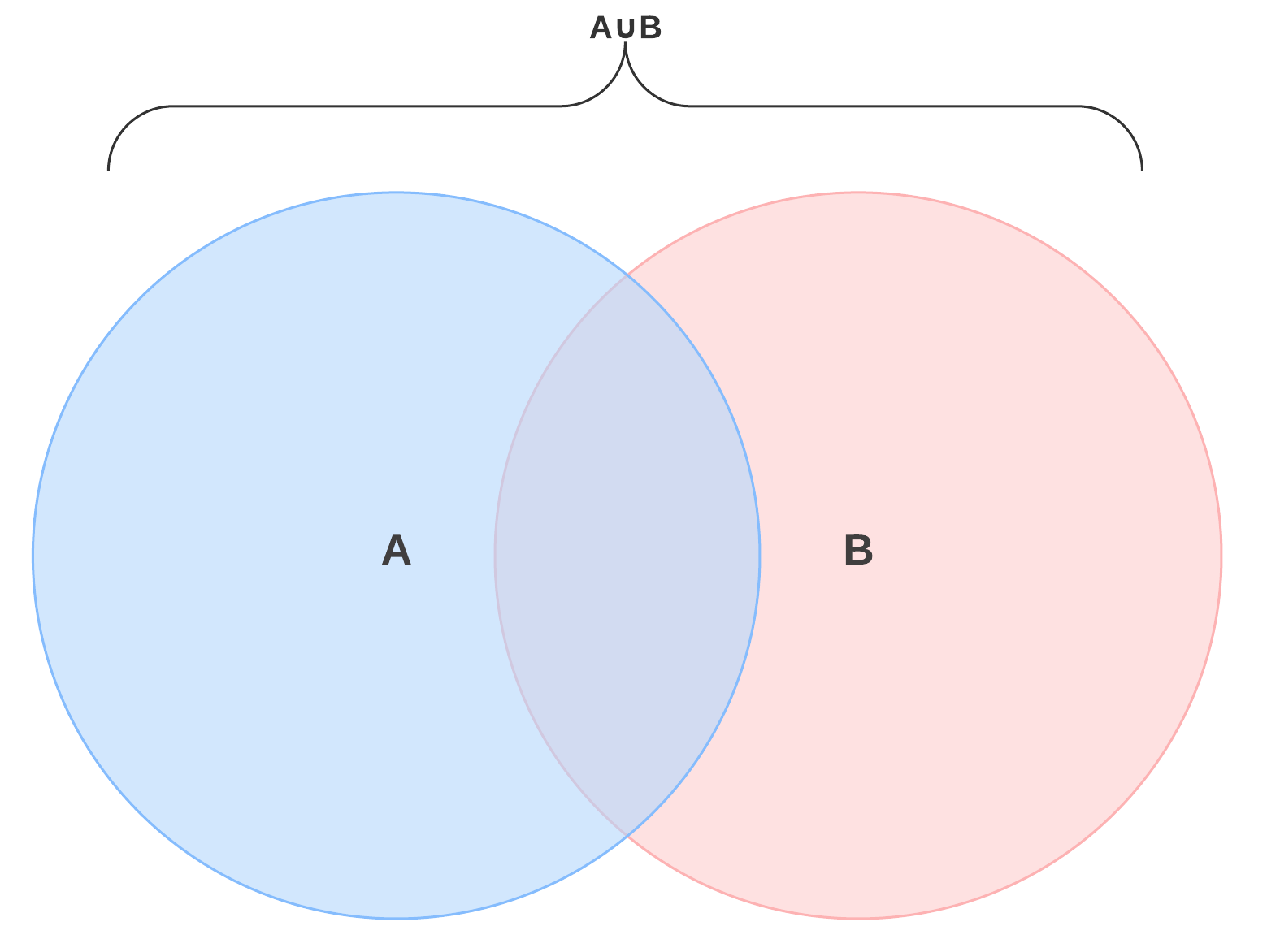
What would the union of two sets look like in the real world? Set A could represent a group of people who play the piano. Set B could represent guitar players. A ∪ B represents those who play piano, guitar, or both.

Intersection of two sets: ∩

In making a Venn diagram, we are often interested in the intersection of two sets—that is, what items are shared between categories. In this diagram, the teal area (where blue and green overlap) represents the intersection of A and B, or A ∩ B.

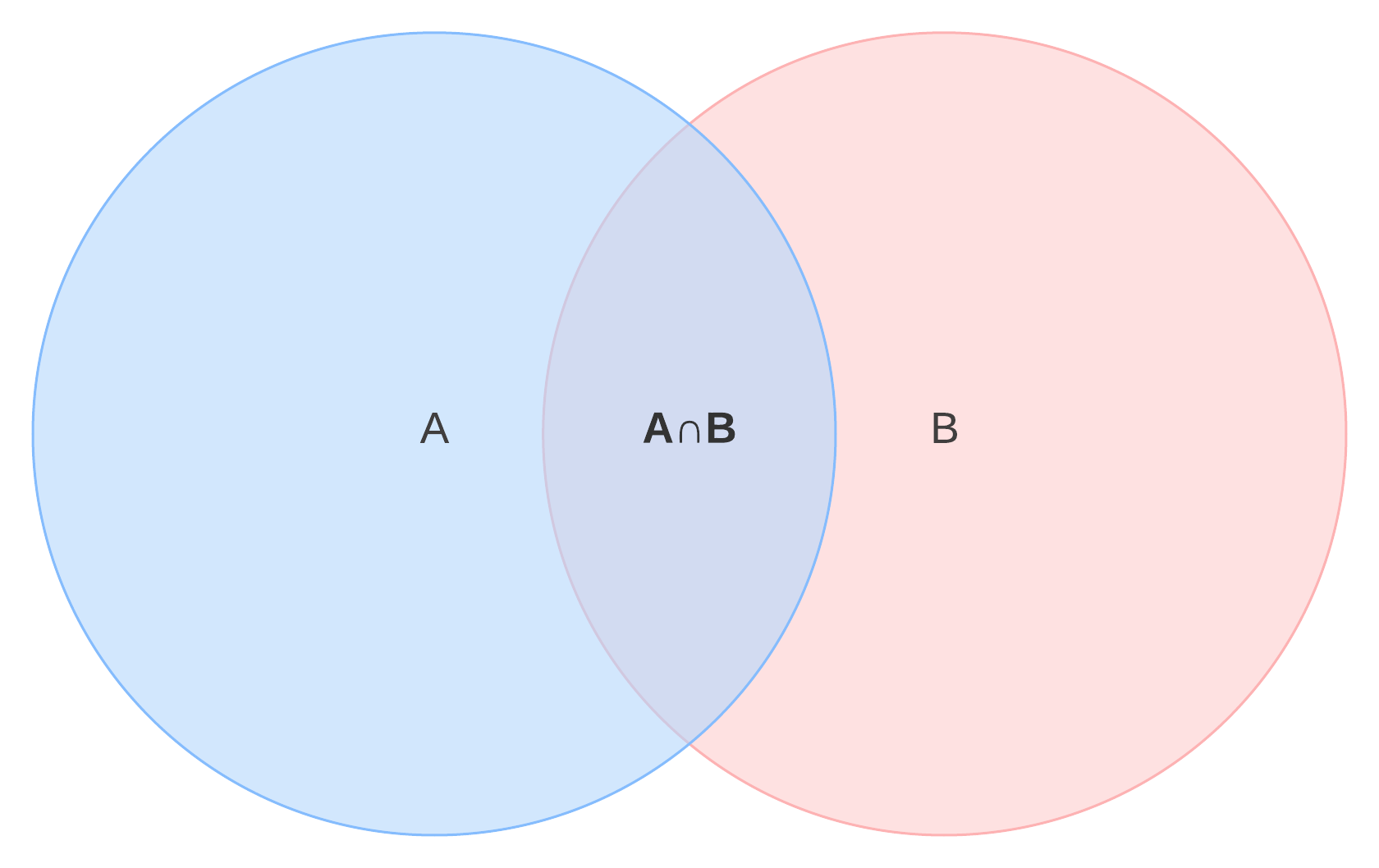
To continue the example, the intersection of piano and guitar players includes those who have mastered both instruments.

Complement of a set: A^c

In making a Venn diagram, you may also want to consider what is not represented in a set. This is the complement of a set, denoted by A∁ (or A′), for set A.

The absolute complement of a set is everything that is not included in the set. This means that given a universe—or a set containing elements of all related sets, denoted by U, the letter this time—everything that is in the universe, except for A, is the absolute complement of A in U. This can be represented by the equation A^c = U \ A.

In the musical instrument case, that would be everyone who does not play the piano.

A fast food Venn diagram illustrating set theory

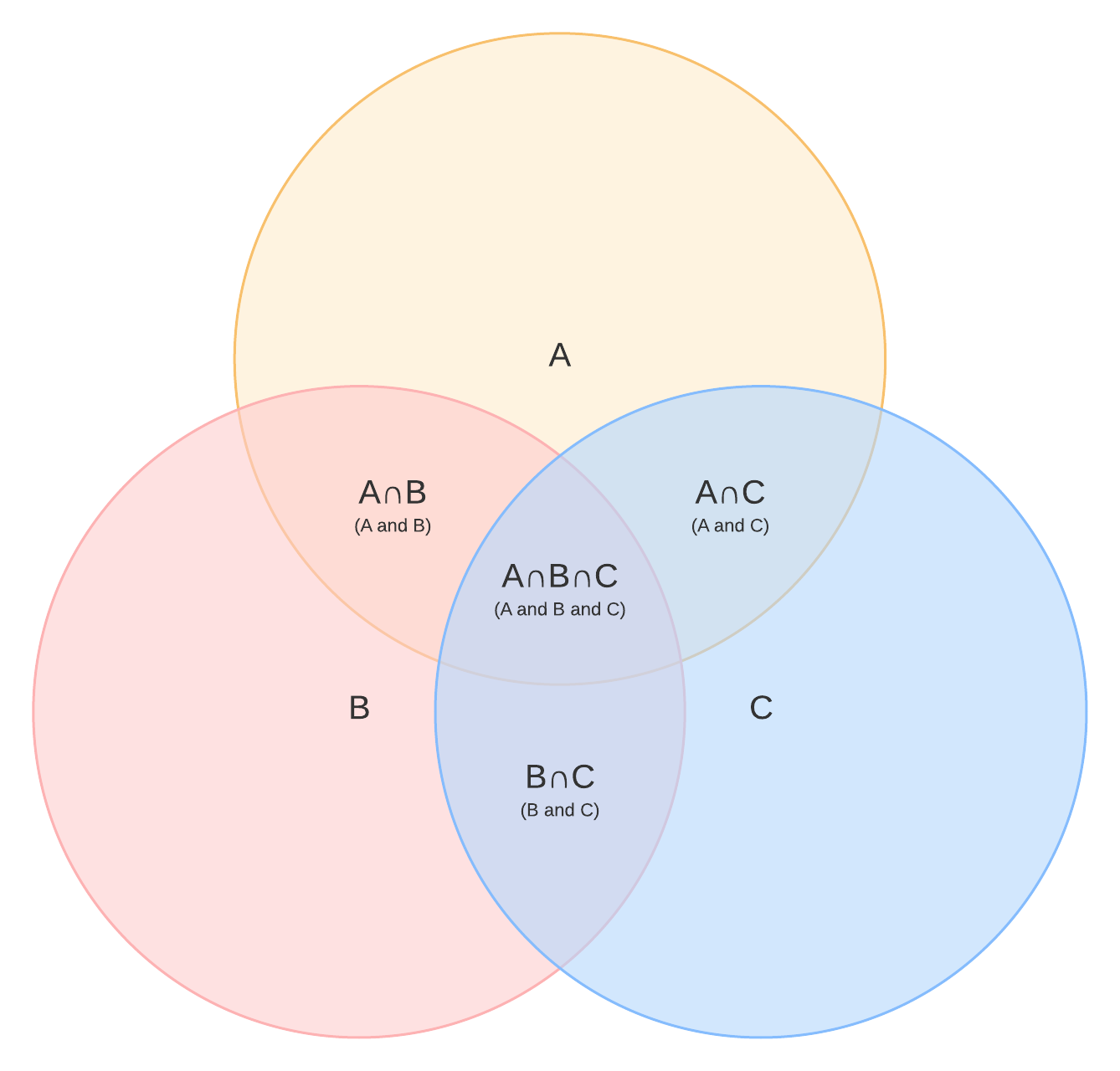
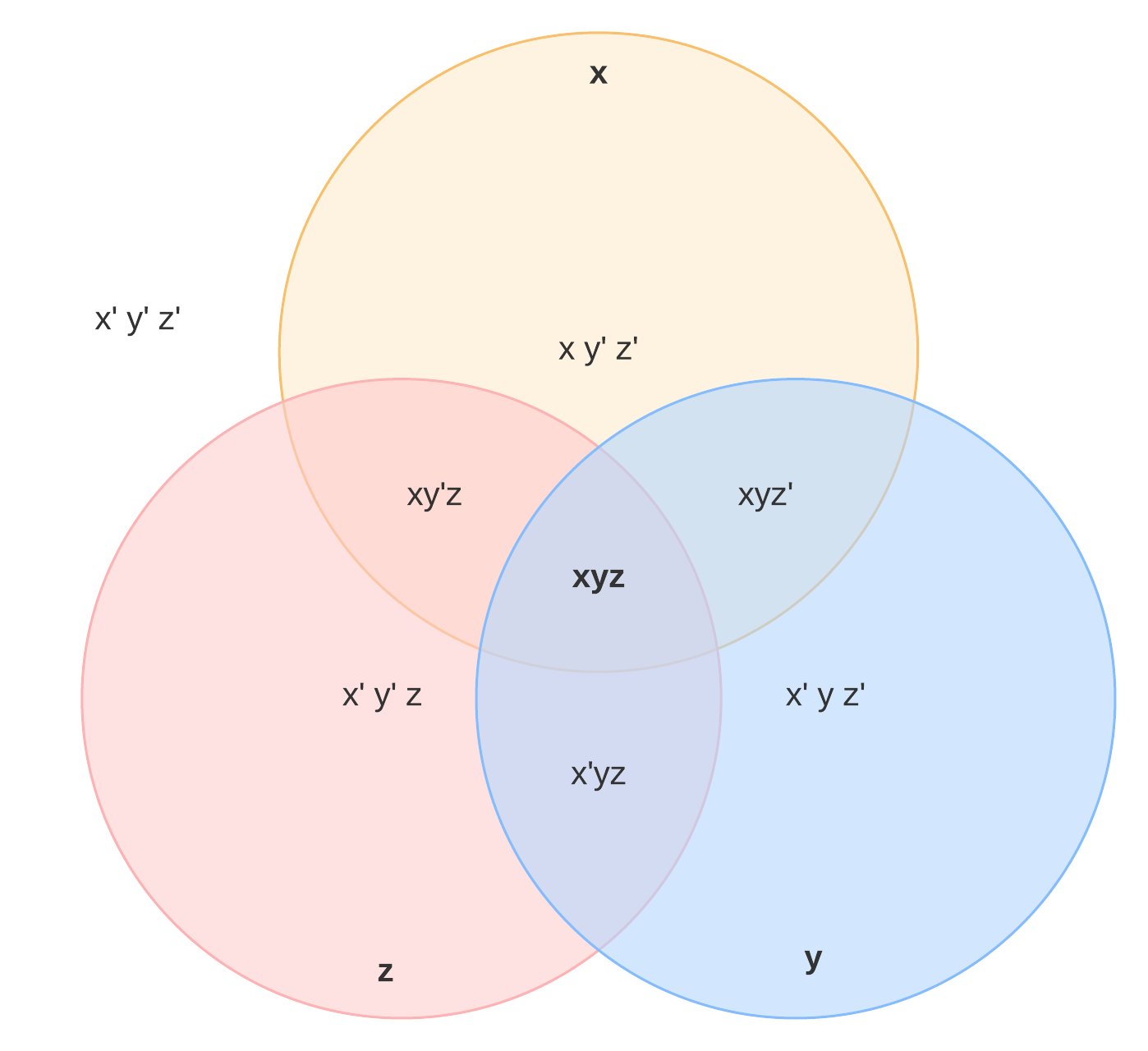
To help you solidify the practical application of set theory, let’s walk through an example. We’ll start with a survey of the fast food preferences of three people. These three people, whom we’ll assign A, B, and C, indicate which restaurants they enjoy. A three-circle diagram covers every possibility: that a restaurant will be chosen by no respondents, one, two, or all three.

Here were the results:

Restaurant	A	B	C
McDonald's	X		X
Wendy's	X	X
Burger King
In-N-Out		X	X
Taco Bell	X		X
KFC
A&W
Chick-fil-A	X	X	X

Now it’s time to create a Venn diagram representing the results. We started with the template below. It uses the symbol we explained, ∩, to show the intersection between two and three sets. There are eight regions that our restaurants could occupy.

Now we fill in our Venn diagram according to the results. In A ∩ B, we have Wendy’s because respondent A and respondent B both chose it. Burger King wasn't chosen by anybody but exists in the universe of available fast food restaurants, so it goes in the white space outside the diagram. The intersection of all three, A ∩ B ∩ C, has Chick-fil-A, since all three respondents chose it.

Here’s what the final diagram looks like:

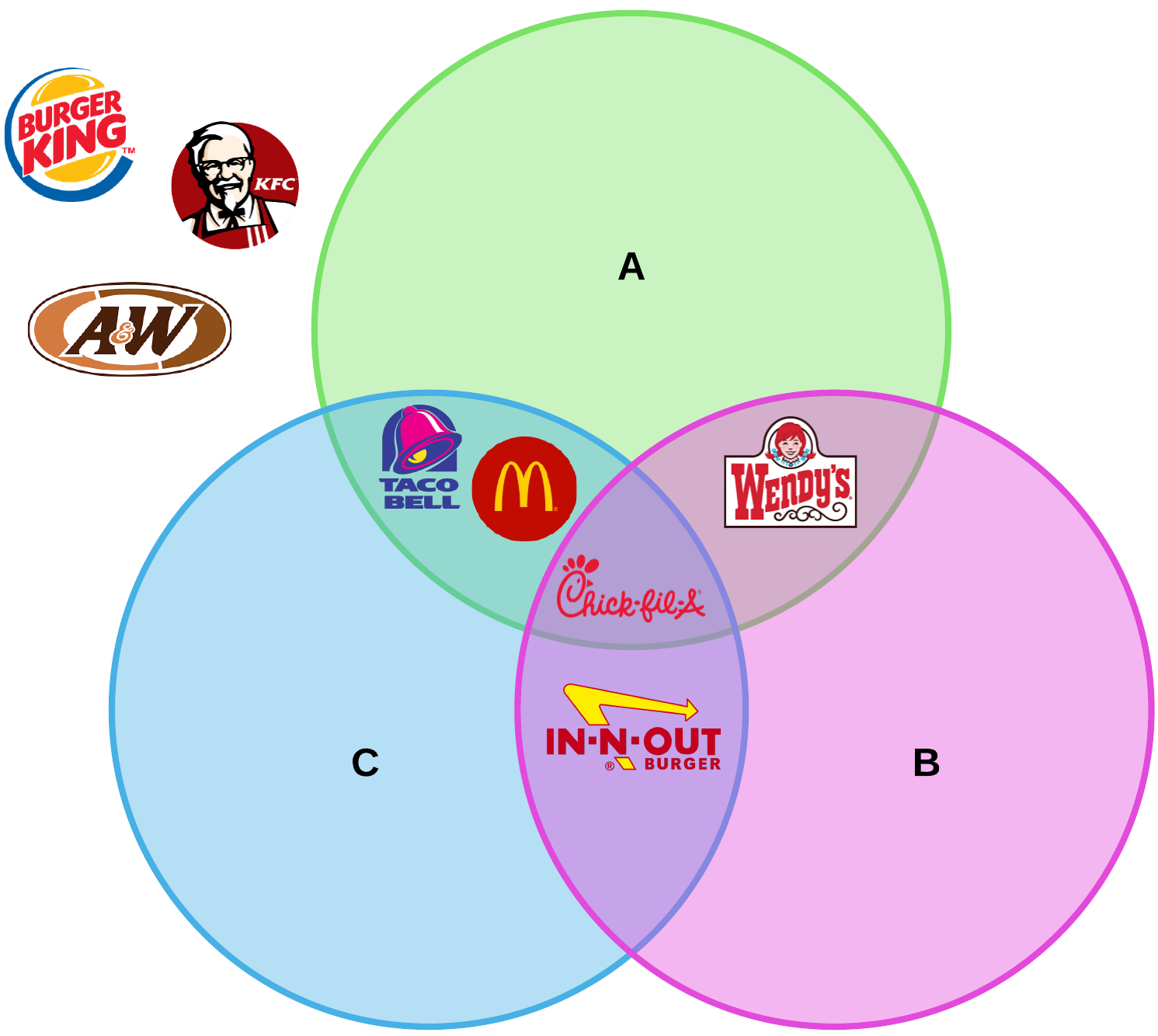
Now we have a visual aid if we are choosing where these three people should go out for lunch!

Now that you've seen a Venn diagram in action, here is an example you can easily customize to create your own! 

Further reading for Venn diagram symbols

If you’re interested in learning more about set theory and creating high-quality Venn diagrams, there are several resources available. For example, the Stanford Encyclopedia has an introduction to Basic Set Theory.

To learn more about the history of Venn diagrams, read our page answering, “What Is a Venn Diagram?” Although John Venn popularized representing set theory with overlapping circles, the ideas and symbols in Venn diagrams actually predate him.

A quick word

If you’ve been following along in Lucidchart, you’ve likely realized that it’s the ideal solution for Venn diagrams. Because you are editing in the cloud, you can easily collaborate with colleagues, import images, and share your diagrams digitally or via print.